
设函数 .
.
(1)求函数 在
在 上的值域;
上的值域;
(2)证明对于每一个 ,在
,在 上存在唯一的
上存在唯一的 ,使得
,使得 ;
;
(3)求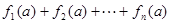 的值.
的值.
(1) 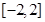 ;(2)证明见解析;(3)当
;(2)证明见解析;(3)当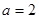 时,为
时,为 ,当
,当 且
且 时,为
时,为 .
.
【解析】
试题分析:(1)由于 可以看作为
可以看作为 的二次函数,故可利用换元法借助二次函数知识求出值域;(2)这类问题的常用方法是证明
的二次函数,故可利用换元法借助二次函数知识求出值域;(2)这类问题的常用方法是证明 在区间
在区间 是单调的,且
是单调的,且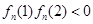 或者
或者 或
或 ,即可得证;本题中证
,即可得证;本题中证 时也可数学归纳法证明;(3)要求
时也可数学归纳法证明;(3)要求 的值,注意分类讨论,
的值,注意分类讨论, 时直接得结论
时直接得结论 ,那么求
,那么求 时,只要用分组求和即可,在
时,只要用分组求和即可,在 时,
时, 中除第一项外是一个公比不为1的等比数列的和,因此先求出
中除第一项外是一个公比不为1的等比数列的和,因此先求出
 ,同样在求
,同样在求 时用分组求和的方法可求得结论.
时用分组求和的方法可求得结论.
试题解析:(1) ,由
,由 令
令 ,
, .
.
 ,
, 在
在 上单调递增,
上单调递增, 在
在 上的值域为
上的值域为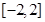 . 4分
. 4分
(2) 对于
对于 ,
, 有
有 ,
,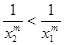 ,从而
,从而 ,
,
 ,
, ,在
,在 上单调递减,
上单调递减,
 ,
, 在
在 上单调递减.
上单调递减.
又 .
.
 . 7分
. 7分
当 时,
时,
(注用数学归纳法证明 相应给分)
相应给分)
又 ,即对于任意自然数
,即对于任意自然数 有
有
 对于每一个
对于每一个 ,存在唯一的
,存在唯一的 ,使得
,使得 11分
11分
(3) .
.
当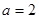 时,
时, .
.
 . 14分
. 14分
当 且
且 时,
时, .
.
 18分
18分
考点:(1)换元法与二次函数的值域;(2)函数的零点;(3)分类讨论与分组求和.


科目:高中数学 来源: 题型:
| px+1 |
| x+1 |
| 1 |
| 2 |
| n |
| cn |
| -1 |
| anSn2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
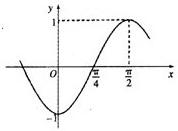 已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示:
已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示:| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 8 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | an |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三3月统一质量检测考试(第二套)理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com