
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为 ![]() .
.
(1)求 ![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 ![]() 的图象,若关于
的图象,若关于 ![]() 的方程
的方程 ![]() 在区间
在区间 ![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液,已知每投放![]() 且
且![]() 个单位的营养液,它在水中释放的浓度
个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中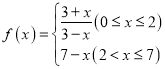 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能持续几天?
(2)若先投放2个单位的营养液,4天后再投放b个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+y2-2x-2y-6=0,以坐标原点O为圆心的圆O与圆M相切.
(1)求圆O的方程;
(2)圆O与x轴交于E,F两点,圆O内的动点D使得DE,DO,DF成等比数列,求![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.
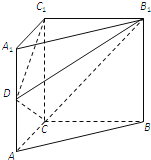
(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,![]() 表示反应距离,
表示反应距离,![]() 表示制动距离,则
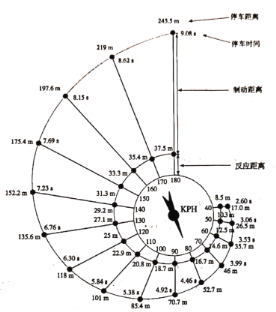
表示制动距离,则![]() .下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
.下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型一:![]() 或模型二:
或模型二:![]() (其中v为汽车速度,a,b
(其中v为汽车速度,a,b
(2)通过计算![]() 时的停车距离,分析选择哪一个函数模型的拟合效果更好.
时的停车距离,分析选择哪一个函数模型的拟合效果更好.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式:  ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1、F2,若椭圆C经过点(0,
(a>b>0)的左、右焦点分别为F1、F2,若椭圆C经过点(0,![]() ),离心率为
),离心率为![]() ,直线l过点F2与椭圆C交于A、B两点.
,直线l过点F2与椭圆C交于A、B两点.
(1)求椭圆C的方程;
(2)若点N为△F1AF2的内心(三角形三条内角平分线的交点),求△F1NF2与△F1AF2面积的比值;
(3)设点A,F2,B在直线x=4上的射影依次为点D,G, E.连结AE,BD,试问当直线l的倾斜角变化时,直线AE与BD是否相交于定点T?若是,请求出定点T的坐标;若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为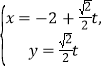 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com