
【题目】已知函数![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 取值范围;
取值范围;
(3)设![]() ,若
,若![]() ,问是否存在实数
,问是否存在实数![]() 使函数
使函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)不存在,理由见解析.
(3)不存在,理由见解析.
【解析】
(1)根据定义域为R且为奇函数可知, ![]() 代入即可求得实数
代入即可求得实数![]() 的值.
的值.
(2)由(1)可得函数![]() 的解析式,并判断出单调性.根据
的解析式,并判断出单调性.根据![]() 将不等式转化为关于
将不等式转化为关于![]() 的不等式,结合
的不等式,结合![]() 时不等式恒成立,即可求得实数
时不等式恒成立,即可求得实数![]() 取值范围;
取值范围;
(3)先用![]() 表示函数
表示函数![]() .根据
.根据![]() 求得
求得![]() 的解析式,根据单调性利用换元法求得
的解析式,根据单调性利用换元法求得![]() 的值域.结合对数的定义域,即可求得
的值域.结合对数的定义域,即可求得![]() 的取值范围.根据对数型复合函数的单调性,即可判断在
的取值范围.根据对数型复合函数的单调性,即可判断在![]() 的取值范围内能否取到最大值0.
的取值范围内能否取到最大值0.
(1)函数![]() 的定义域为R,且为奇函数
的定义域为R,且为奇函数
所以![]() ,即
,即![]()
解得![]()
(2)由(1)可知当![]() 时,
时, ![]()
因为![]() ,即
,即![]()
![]()
解不等式可得![]()
所以![]() 在R上单调递减,且
在R上单调递减,且![]()
所以不等式![]() 可转化为
可转化为![]()
根据函数![]() 在R上单调递减
在R上单调递减
所不等式可化为![]()
即不等式![]() 在
在![]() 恒成立
恒成立
所以![]()
![]() 恒成立
恒成立
化简可得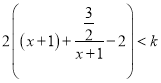
由打勾函数的图像可知,当![]() 时,
时,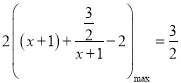
所以![]()
(3)不存在实数![]() .理由如下:
.理由如下:
![]()
![]()
因为![]()
![]()
代入可得![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
则![]() ,
,
令![]() ,易知
,易知![]() 在R上为单调递增函数
在R上为单调递增函数
所以当![]() 时,
时, ![]() ,
,![]()
则![]()
根据对数定义域的要求,所以![]() 满足
满足![]() 在
在![]() 上恒成立
上恒成立
即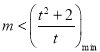 在
在![]() 上恒成立
上恒成立
令![]() ,
,![]()
所以![]() ,即
,即![]()
又因为![]()
所以![]()
对于二次函数![]() ,开口向上,对称轴为
,开口向上,对称轴为![]()
因为![]()
所以![]()
所以对称轴一直位于![]() 的左侧,即二次函数
的左侧,即二次函数![]() 在
在![]() 内单调递增
内单调递增
所以![]() ,
,![]()
假设存在满足条件的实数![]() ,则:
,则:
当![]() 时, 由复合函数单调性的判断方法,可知
时, 由复合函数单调性的判断方法,可知![]() 为减函数,所以根据
为减函数,所以根据![]() 可知
可知![]() ,即
,即![]()
解得![]() ,所以舍去
,所以舍去
当![]() 时, 复合函数单调性的判断方法可知
时, 复合函数单调性的判断方法可知![]() 为增函数,所以根据
为增函数,所以根据![]() 可知
可知![]() ,即
,即![]()
解得![]() ,所以舍去
,所以舍去
综上所述,不存在实数![]() 满足条件成立.
满足条件成立.


科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.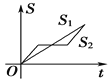 B.
B.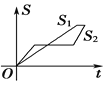 C.
C.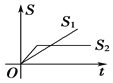 D.
D.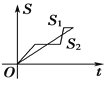
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元.设该公司的仪器月产量为![]() 台,当月产量不超过400台时,总收益为
台,当月产量不超过400台时,总收益为![]() 元,当月产量超过400台时,总收益为
元,当月产量超过400台时,总收益为![]() 元.(注:总收益=总成本+利润)
元.(注:总收益=总成本+利润)
(1)将利润表示为月产量![]() 的函数
的函数![]() ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为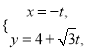 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线
分别交直线![]() 和曲线
和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应
的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为![]() 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留
平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留![]() 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为
米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为![]() 米,如图所示.
米,如图所示.

(1)将两个养殖池的总面积![]() 表示
表示![]() 为的函数,并写出定义域;
为的函数,并写出定义域;
(2)当温室的边长![]() 取何值时,总面积
取何值时,总面积![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过函数性质的学习,我们知道:“函数![]() 的图象关于
的图象关于![]() 轴成轴对称图形”的充要条件是“
轴成轴对称图形”的充要条件是“![]() 为偶函数”.
为偶函数”.
(1)若![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某数学学习小组针对上述结论进行探究,得到一个真命题:“函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称图形”的充要条件是“
成轴对称图形”的充要条件是“![]() 为偶函数”.若函数
为偶函数”.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 图像上任意一点
图像上任意一点![]() 处的切线的斜率
处的切线的斜率![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若对于区间![]() 上任意两个不相等的实数
上任意两个不相等的实数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com