
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() .
.
(1)写出曲线![]() ,
, ![]() 的普通方程;
的普通方程;
(2)过曲线![]() 的右焦点
的右焦点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,该直线与曲线
,该直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在x轴上,点 ![]() 在圆C上,圆心到直线2x﹣y=0的距离为
在圆C上,圆心到直线2x﹣y=0的距离为 ![]() ,则圆C的方程为( )
,则圆C的方程为( )
A.(x﹣2)2+y2=3
B.(x+2)2+y2=9
C.(x±2)2+y2=3
D.(x±2)2+y2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C的对边分别为a、b、c.己知c= ![]() asinC﹣ccosA.
asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为x(m),三块种植植物的矩形区域的总面积为S(m2). 
(1)求S关于x的函数关系式;
(2)求S的最大值,及此时长X的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB= ![]() ,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过原点O,与x轴另一交点的横坐标为4,与y轴另一交点的纵坐标为2,
(1)求圆C的方程;
(2)已知点B的坐标为(0,2),设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的焦点在x轴上,离心率等于 ![]() ,且过点(1,
,且过点(1, ![]() ). (Ⅰ)求椭圆C的标准方程;
). (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于M点,若 ![]() =λ1
=λ1 ![]() ,
, ![]() =λ2
=λ2 ![]() ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双流中学校运动会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以 下(不包括175
以 下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.
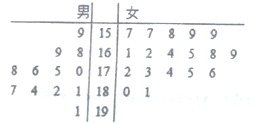
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com