
【题目】全国大学生机器人大赛是由共青团中央,全国学联,深圳市人民政府联合主办的赛事,是中国最具影响力的机器人项目,是全球独创的机器人竞技平台.全国大学生机器人大赛比拼的是参赛选手们的能力,坚持和态度,展现的是个人实力以及整个团队的力量.2015赛季共吸引全国240余支机器人战队踊跃报名,这些参赛战队来自全国六大赛区,150余所高等院校,其中不乏北京大学,清华大学,上海交大,中国科大,西安交大等众多国内顶尖高校,经过严格筛选,最终由111支机器人战队参与到2015年全国大学生机器人大赛的激烈角逐之中,某大学共有“机器人”兴趣团队1000个,大一、大二、大三、大四分别有100,200,300,400个,为挑选优秀团队,现用分层抽样的方法,从以上团队中抽取20个团队.
(1)应从大三抽取多少个团队?
(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的分数如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
从甲、乙两组中选一组强化训练,备战机器人大赛.
(i)从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?
(ii)从乙组中不低于140分的团队中任取两个团队,求至少有一个团队为144分的概率.
【答案】(1)6个(2)(i)选乙队理由: ![]() ,且乙队中不低于140分的团队多,在竞技比赛中,高分团队获胜的概率大(ii)
,且乙队中不低于140分的团队多,在竞技比赛中,高分团队获胜的概率大(ii)![]()
【解析】试题分析:
(1)由题意可知大三团队个数占总团队数的![]() ,则应从大三中抽取
,则应从大三中抽取![]() 个团队.
个团队.
(2)(i)分别计算甲乙两组数据的平均值和方差, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由于
,由于![]() ,可知选择甲组有利,成绩波动小;由于
,可知选择甲组有利,成绩波动小;由于![]() ,可知选择乙组有利,在竞技比赛中,高分团队获胜的概率大.
,可知选择乙组有利,在竞技比赛中,高分团队获胜的概率大.
(ii)不低于140分的团队共5个,其中140分的团队有3个,144分的团队有2个,据此可得任取两个的情况有10个,其中两个团队都是140分的情况有3个,由对立事件概率公式可得至少有一个团队为144分的概率为![]() .
.
试题解析:
(1)由题知,大三团队个数占总团队数的![]() ,
,
则用分层抽样的方法,应从大三中抽取![]() 个团队.
个团队.
(2)(i)甲组数据的平均数![]() ,乙组数据的平均数
,乙组数据的平均数![]() ,
,
甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,
,
选甲队理由:甲、乙两队平均数相差不大,且![]() ,甲组成绩波动小.
,甲组成绩波动小.
选乙队理由: ![]() ,且乙队中不低于140分的团队多,在竞技比赛中,高分团队获胜的概率大.
,且乙队中不低于140分的团队多,在竞技比赛中,高分团队获胜的概率大.
(ii)不低于140分的团队共5个,其中140分的团队有3个,分别为![]() ,
, ![]() ,
, ![]() ,144分的团队有2个,分别为
,144分的团队有2个,分别为![]() ,
, ![]() ,
,
则任取两个的情况有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10个,
,共10个,
其中两个团队都是140分的情况有![]() ,
, ![]() ,
, ![]() ,共3个.
,共3个.
故所求概率![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】用0, 1, 2, 3, 4, 5这六个数字, 可以组成______个无重复数字的三位数, 也可以组成______个能被5整除且无重复数字的五位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
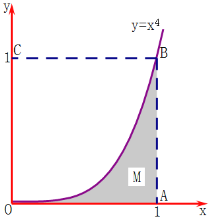
【题目】Monte-Carlo方法在解决数学问题中有广泛的应用.下面利用Monte-Carlo方法来估算定积分![]() .考虑到
.考虑到![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,直线
轴,直线![]() 所围成的区域
所围成的区域![]() 的面积,如图,在
的面积,如图,在![]() 外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
(1)求X的期望![]() 和方差
和方差![]() ;
;
(2)求用以上方法估算定积分![]() 时,
时,![]() 的估计值与实际值之差在区间(-0.01,0.01)的概率.
的估计值与实际值之差在区间(-0.01,0.01)的概率.
附表:![]()
| 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,过点
,过点![]() 、
、![]() 分别作两平行直线
分别作两平行直线![]() 、
、![]() ,
, ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点, ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且当直线
两点,且当直线![]() 过右焦点和上顶点时,四边形
过右焦点和上顶点时,四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若四边形![]() 是菱形,求正数
是菱形,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,其中i为虚数单位,当实数m取何值时,复数z对应的点:
(1)位于虚轴上;
(2)位于一、三象限;
(3)位于以原点为圆心,以4为半径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() 的右焦点为F,过点F且斜率为k的直线与椭圆Γ交于A(x1, y1)、B(x2, y2)两点(点A在x轴上方),点A关于坐标原点的对称点为P,直线PA、PB分别交直线l:x=4于M、N两点,记M、N两点的纵坐标分别为yM、yN.
的右焦点为F,过点F且斜率为k的直线与椭圆Γ交于A(x1, y1)、B(x2, y2)两点(点A在x轴上方),点A关于坐标原点的对称点为P,直线PA、PB分别交直线l:x=4于M、N两点,记M、N两点的纵坐标分别为yM、yN.
(1) 求直线PB的斜率(用k表示);
(2) 求点M、N的纵坐标yM、yN (用x1, y1表示) ,并判断yM yN是否为定值?若是,请求出该定值;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com