
分析 根据题意,设出点A、B的坐标,利用AB=2得出方程①;再写出向量$\overline{AP}$+$\overline{BP}$+$\overline{OP}$的坐标表示,求出${(\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP})}^{2}$的取值范围,即可得出|$\overline{AP}$+$\overline{BP}$+$\overline{OP}$|的取值范围.
解答 解:根据题意,设点A(x1,0),B(0,y2),
AB=2,∴${{x}_{1}}^{2}$+${{y}_{2}}^{2}$=4①;
由点P(2,$\sqrt{5}$),
∴$\overline{AP}$+$\overline{BP}$+$\overline{OP}$=(2-x1$\sqrt{5}$)+(2$\sqrt{5}$-y2)+(2$\sqrt{5}$)
=(6-x1,3$\sqrt{5}$-y2);
∴${(\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{OP})}^{2}$=${(6{-x}_{1})}^{2}$+${(3\sqrt{5}{-y}_{2})}^{2}$
=81-12x1-6$\sqrt{5}$y2+(${{x}_{1}}^{2}$+${{y}_{2}}^{2}$)
=85-12x1-6$\sqrt{5}$y2②;
设$\left\{\begin{array}{l}{{x}_{1}=2cosθ}\\{{y}_{2}=2sinθ}\end{array}\right.$,θ∈[0,2π);
则85-12x1-6$\sqrt{5}$y2=85-24cosθ-12$\sqrt{5}$sinθ
=85-36sin(θ+α),其中α=tan$\frac{\sqrt{5}}{2}$;
∴当sin(θ+α)=1时,|$\overline{AP}$+$\overline{BP}$+$\overline{OP}$|取得最小值$\sqrt{85-36}$=7,
当sin(θ+α)=-1时,|$\overline{AP}$+$\overline{BP}$+$\overline{OP}$|取得最大值$\sqrt{85+36}$=11;
∴|$\overline{AP}$+$\overline{BP}$+$\overline{OP}$|的取值范围是[7,11].
故答案为:[7,11].
点评 本题考查了平面向量的应用问题,也考查了求向量模长的应用问题,考查了转化思想的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | [4,+∞) | C. | (5,+∞) | D. | [5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 是否公平 | 男 | 女 |
| 公平 | 40 | 30 |
| 不公平 | 160 | 270 |
| P(K2≥k) | 0.000 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
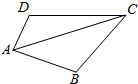 如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.
如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com