
已知![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() ;
;
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右焦点![]() 作直线l交椭圆于A、B两点,交y轴于M点,若
作直线l交椭圆于A、B两点,交y轴于M点,若
![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
(08年青岛市质检二文)(14分) 已知![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() ;
;
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年青岛市质检二理) (14分) 已知![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() ;
;
(Ⅰ)求椭圆的标准方程;
(Ⅱ)⊙![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() (
(![]() 为整数)与⊙
为整数)与⊙![]() 相切,并与椭圆交
相切,并与椭圆交
于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试理科数学试卷(解析版) 题型:解答题
已知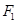 、
、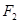 是椭圆
是椭圆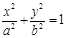
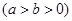 的左、右焦点,且离心率
的左、右焦点,且离心率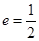 ,点
,点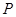 为椭圆上的一个动点,
为椭圆上的一个动点,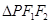 的内切圆面积的最大值为
的内切圆面积的最大值为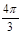 .
.
(1) 求椭圆的方程;
(2) 若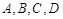 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量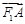 与
与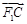 共线,
共线,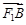 与
与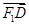 共
共
线,且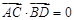 ,求
,求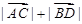 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省长春市毕业班第四次调研测试文科数学试卷(解析版) 题型:解答题
已知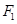 、
、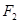 是椭圆
是椭圆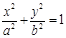
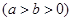 的左、右焦点,且离心率
的左、右焦点,且离心率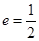 ,点
,点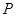 为椭圆上的一个动点,
为椭圆上的一个动点,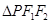 的内切圆面积的最大值为
的内切圆面积的最大值为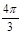 .
.
(1) 求椭圆的方程;
(2) 若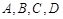 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量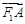 与
与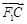 共线,
共线,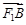 与
与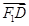 共
共
线,且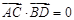 ,求
,求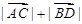 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com