
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形.若存在,求出点
为底边的等腰三角形.若存在,求出点![]() 的横坐标的取值范围,若不存在,请说明理由.
的横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2. 
(1)求证:平面PAC⊥平面PCD;
(2)若E是PD的中点,求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1= ![]() ,P、Q分别是AB、AC上的点,且PQ∥BC.
,P、Q分别是AB、AC上的点,且PQ∥BC. 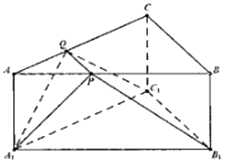
(1)若平面A1PQ与平面A1B1C1相交于直线l,求证:l∥B1C1;
(2)当平面A1PQ⊥平面PQC1B1时,确定点P的位置并说明理由.S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示. 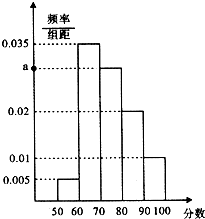
(1)求a值及这100名考生的平均成绩;
(2)若该单位决定在成绩较高的第三、四、五组中按分层抽样抽取6名考生进入第二轮面试,现从这6名考生中抽取3名考生接受单位领导面试,设第四组中恰有1名考生接受领导面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com