
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(1)完成下面的频率分布表;
(2)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(3)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.
分组 | 频数 | 频率 |
[41,51) | 2 |
|
[51,61) | 3 |
|
[61,71) | 4 |
|
[71,81) | 6 |
|
[81,91) | ||
[91,101) | 3 | |
[101,111) |
|
![]()
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据已知条件中的数据,得到频数,计算求得对应频率,从而补全频率分布表;(2)根据频率分布表求得频率分布直方图缺失的矩形的高,从而补全图形;再根据![]() 的频率计算得到矩形的高
的频率计算得到矩形的高![]() ;(3)列出所有基本事件,找到符合题意的基本事件个数,利用古典概型求出结果.
;(3)列出所有基本事件,找到符合题意的基本事件个数,利用古典概型求出结果.
(1)需补全的数据如下图所示:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
(2)补全频率分布直方图,如下图所示:

由已知,空气质量指数在区间![]() 的频率为
的频率为![]()
![]()
(3)设![]() 表示事件“在本月空气质量指数大于等于
表示事件“在本月空气质量指数大于等于![]() 的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间
的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间![]() 内”
内”
由已知得:质量指数在区间![]() 内的有
内的有![]() 天,记这三天分别为
天,记这三天分别为![]()
质量指数在区间![]() 内的有
内的有![]() 天,记这两天分别为
天,记这两天分别为![]()
则选取的所有可能结果为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,即基本事件数为
,即基本事件数为![]()
事件“至少有一天空气质量指数在区间![]() 内”的可能结果为:
内”的可能结果为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
基本事件数为![]()
![]()


科目:高中数学 来源: 题型:
【题目】如图,正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是

A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校调查了20个班中有网上购物经历的人数,得到了如图所示的茎叶图,以![]() 为分组,作出这组数的频率分布直方图,并说明频率分布直方图与茎叶图之间的关系.
为分组,作出这组数的频率分布直方图,并说明频率分布直方图与茎叶图之间的关系.
0 1 2 3 | 7 3 7 6 4 4 3 0 7 5 5 4 3 2 0 8 5 4 3 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过椭圆
经过椭圆![]() 的右顶点
的右顶点![]() 、下顶点
、下顶点![]() 和上顶点
和上顶点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)直线![]() 经过点
经过点![]() 且与
且与![]() 垂直,
垂直,![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=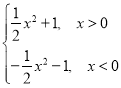
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com