
【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
【答案】(1)7;(2)3455;(3)见解析.
【解析】(1)根据题意,将两数列对应代入计算,问题即可得解;(2)由题意,根据递推关系,不难发现数列![]() 是以4为周期的数列,由此可确定数列
是以4为周期的数列,由此可确定数列![]() 亦为周期数列,由其首项即可知对应数列各项,依据定义当项数
亦为周期数列,由其首项即可知对应数列各项,依据定义当项数![]() 越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
试题解析:(1)由题得数列1,3,5,6和数列2,3,10,7的距离为7.
(2)设![]() ,其中
,其中![]() 且
且![]() .
.
由![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,….
,….
所以![]() ,
, ![]() ,….
,….
因此集合![]() 中的所有数列都具有周期性,且周期为4.
中的所有数列都具有周期性,且周期为4.
所以数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
,
数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .
.
因为![]() ,
,
所以项数![]() 越大,数列
越大,数列![]() 和
和![]() 的距离越大.
的距离越大.
因为![]() ,
,
而![]()
![]() ,
,
因此,当![]() 时,
时, ![]() .
.
故![]() 的最大值为3455.
的最大值为3455.
(3)假设![]() 中的元素个数大于或等于17.
中的元素个数大于或等于17.
因为数列![]() 中,
中, ![]() 或1,
或1,
所以仅由数列前三项组成的数组(![]() ,
, ![]() ,
, ![]() )有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
)有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
那么这17个元素之中必有3个具有相同的![]() ,
, ![]() ,
, ![]() .
.
设这3个元素分别为![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() .
.
因为这3个元素中每两个元素的距离大于或等于3,
所以在![]() 与
与![]() 中,
中, ![]()
![]() 至少有3个成立.
至少有3个成立.
不妨设![]() ,
, ![]() ,
, ![]() .
.
由题意得![]() ,
, ![]() 中一个等于0,另一个等于1.
中一个等于0,另一个等于1.
又因为![]() 或1,所以
或1,所以![]() 和
和![]() 中必有一个成立.
中必有一个成立.
同理得: ![]() 和
和![]() 中必有一个成立,
中必有一个成立, ![]() 和
和![]() 中必有一个成立,
中必有一个成立,
所以“![]()
![]() 中至少有两个成立”和“
中至少有两个成立”和“![]()
![]() 中至少有两个成立”中必有一个成立.
中至少有两个成立”中必有一个成立.
故![]() 和
和![]() 中必有一个成立,这与题意矛盾.
中必有一个成立,这与题意矛盾.
所以![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵。某汽车经销商推出![]() 三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图。已知从
三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图。已知从![]() 三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元。以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率。
三种分期付款销售中,该经销商每销售此品牌汽车1辆所获得的利润分别是1万元,2万元,3万元。以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率。

(Ⅰ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润不大于2万元的概率;
(Ⅱ)求采用上述分期付款方式销售此品牌汽车1辆,该汽车经销商从中所获得的利润的平均值;
(Ⅲ)根据某税收规定,该汽车经销商每月(按30天计)上交税收的标准如下表:
![]()
若该经销商按上述分期付款方式每天平均销售此品牌汽车3辆,估计其月纯收入(纯收入=总利润-上交税款)的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年五一假期期间,高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
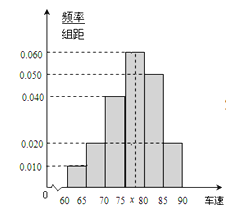
(Ⅰ)求这40辆小型车辆车速的众数和中位数以及平均数的估计值.
(Ⅱ)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级开设五门大学先修课程,其中属于数学学科的有两门,分别是线性代数和微积分,其余三门分别为大学物理,商务英语以及文学写作,年级要求每名学生只能选修其中一科,该校高二年级600名学生各科选课人数统计如下表:

其中选修数学学科的人数所占频率为0.6,为了了解学生成绩与选课情况之间的关系,用分层抽样的方法从这600名学生中抽取10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(2)从选出的10名学生中随机抽取3人,记![]() 为选择线性代数人数与选择微积分人数差的绝对值,求随机变量
为选择线性代数人数与选择微积分人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
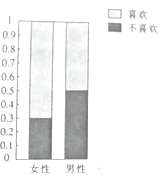
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
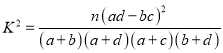 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.

(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com