
【题目】已知{an}是等差数列,{bn}是等比数列,Sn为数列{an}的前n项和,a1=b1=1,且b3S3=36,b2S2=8(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)若an<an+1 , 求数列{anbn}的前n项和Tn .
【答案】
(1)解:设等差数列{an}的公差为d,等比数列{bn}的公比为q,
∵a1=b1=1,且b3S3=36,b2S2=8(n∈N*).
∴ ![]() ,解得
,解得 ![]() 或
或 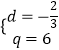 .
.
∴an=2n﹣1,bn=2n﹣1;或an=1﹣ ![]() (n﹣1)=
(n﹣1)= ![]() ,bn=6n﹣1
,bn=6n﹣1
(2)解:∵an<an+1,∴由(1)知an=2n﹣1, ![]() .
.
∴ ![]() .
.
∴2Tn=2+3×22+5×23+…+(2n﹣3)×2n﹣1+(2n﹣1)×2n,
∴﹣Tn=1+2(2+22+…+2n﹣1)﹣(2n﹣1)×2n=1+ ![]() ﹣(2n﹣1)×2n=﹣(2n﹣3)×2n﹣3.
﹣(2n﹣1)×2n=﹣(2n﹣3)×2n﹣3.
∴Tn=(2n﹣3)×2n+3.(n∈N*)
【解析】(1)利用等差数列与等比数列的通项公式及其求和公式即可得出.(2)an<an+1 , 由(1)知an=2n﹣1, ![]() .利用“错位相减法”与等比数列的求和公式即可得出.
.利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系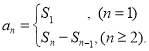 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
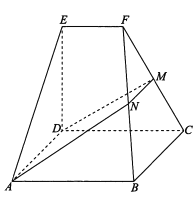
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 值;若不能,说明理由。
值;若不能,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为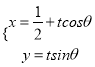 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线m、n与平面α、β,下列命题正确的是( )
A.m⊥α,n∥β且α⊥β,则m⊥n
B.m⊥α,n⊥β且α⊥β,则m⊥n
C.α∩β=m,n⊥m且α⊥β,则n⊥α
D.m∥α,n∥β且α∥β,则m∥n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1 , E,F,P,Q分别是BC,C1D1 , AD1 , BD的中点,求证:
(1)PQ∥平面DCC1D1
(2)EF∥平面BB1D1D.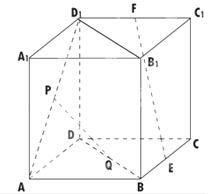
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com