
(Ⅰ)求a3和b3的值;
(Ⅱ)求an及bn的表达式;
(Ⅲ)对an个整点用红、黄、蓝、白四色之一着色,其方法总数为An,对bn个整点用红、黄两色之一着色,其方法总数为Bn,试比较An与Bn的大小.
解:(Ⅰ)n=3时,直线x=0上有点(0,0)(0,1)(0,2)(0,3),直线x=1上有点(1,0)(1,1)(1,2),直线x=2上有点(2,0)(2,1),直线x=3上有点(3,0),所以a3=1,b3=4+3+2+1=10.
(Ⅱ)解:n=1时,b1=3,a1=0,n=2时,b1=6,a2=0,
当n≥3时,bn=(n+1)+n+(n-1)+…+2+1=![]() ,an=bn-3(n+1)+3=
,an=bn-3(n+1)+3=![]() ,
,
当n=1,2时也满足
所以an=![]() ,bn=
,bn=![]() (n∈N*).
(n∈N*).
(Ⅲ)对于an个整点中的每一个点都有4种着色方法,故An=![]()
对于bn个整点中的每一个点都有2种着色方法,故Bn=![]()
![]() =
=![]() =
=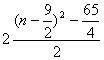 .
.
当n=1,2,3,4,5,6,7,8时An<Bn,
当n≥9且n∈N*时,An>Bn.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
| A、3 | B、4 | C、2和5 | D、3和4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+1 |
| an |
| an+1 |
| an |
| an |
| an-1 |
| a1 |
| 3! |
| a2 |
| 4! |
| a3 |
| 5! |
| an |
| (n+2)! |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com