练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学校高一学生有1000名学生参加一次数学小测验，随机抽取200名学生的测验成绩得如图所示的频率分布直方图：

    （1）求该学校高一学生随机抽取的200名学生的数学平均成绩和标准差（同一组中的数据用该组区间的中点值做代表）；

    （2）试估计该校高一学生在这一次的数学测验成绩在区间之内的概率是多少？测验成绩在区间之外有多少位学生？（参考数据：）

    【答案】（1）平均数，样本标准差.（2）概率为0.9356，全校测验成绩在区间之外约有64（人）

    【解析】

    （1）根据频率分布直方图中平均数小矩形底边中点乘以小矩形的面积之和；利用方差公式可求方差，进而可求标准差.

    （2）由（1）知，由频率分布直方图求出的概率即可求解.

    （1）数学成绩的样本平均数为：

    ，

    数学成绩的样本方差为：

    .

    所以估计这批产品质量指标值的样本平均数，

    样本标准差.

    （2）由（1）知，

    则

    ，

    所以（人）

    所以估计该学校在这一次的数学测验中成绩在区间之内的概率为0.9356，全校测验成绩在区间之外约有64（人）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数存在与直线平行的切线，求实数的取值范围；

    （2）设，若有极大值点，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y = f(x)是定义域为R的偶函数，当x≥0时，函数f(x)的图象是由一段抛物线和一条射线组成（如图所示）．

    ①当时，y的取值范围是______；

    ②如果对任意 (b <0)，都有，那么b的最大值是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义在上的函数，若存在实数及、（）使得对于任意 都有成立，则称函数是带状函数；若存在最小值，则称为带宽.

    （1）判断函数 是不是带状函数？如果是，指出带宽（不用证明）；如果不是，请说明理由；

    （2）求证：函数（）是带状函数；

    （3）求证：函数是带状函数的充要条件是.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，若分别是棱的中点，则必有（ ）

    A.

    B.

    C. 平面平面

    D. 平面平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AOB是一块半径为r的扇形空地，．某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH，剩余的地方进行绿化．若，设

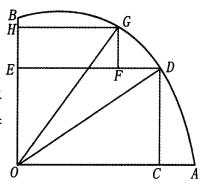
    (Ⅰ)记活动场地与停车场占地总面积为，求的表达式；

    (Ⅱ)当为何值时，可使活动场地与停车场占地总面积最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将平面上每个点都以红、蓝两色之一着色，证明：存在这样的两个相似三角形，它们的相似比为1995，并且每一个三角形的三个顶点同色。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在区间上的值域.

    (1)求的值；

    (2)若不等式在上恒成立，求实数的取值范围；

    (3)若函数有三个零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，圆的方程为，点为圆上的动点，过点的直线被圆截得的弦长为．

    (1)求直线的方程；

    (2)求面积的最大值．

    查看答案和解析>>

    同步练习册答案