
| 城市 | 民营企业数量 | 抽取数量 |
| A | 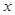 | 4 |
| B | 28 |  |
| C | 84 | 6 |
 、
、 的值;
的值;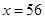 ,
,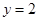 ;(2)
;(2)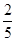 .
.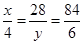 , 4分
, 4分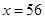 ,
,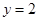 6分
6分 ,从城市B抽取的民营企业分别为
,从城市B抽取的民营企业分别为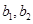 . 则从城市A、B抽取的6个中再随机选2个进行跟踪式调研的基本事件有
. 则从城市A、B抽取的6个中再随机选2个进行跟踪式调研的基本事件有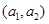 ,
,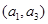 ,
,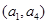 ,
,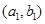 ,
,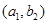 ,
,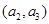 ,
, ,
,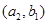 ,
,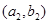 ,
,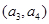 ,
,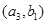 ,
,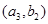 ,
,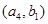 ,
,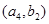 ,
,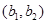 共15个 8分
共15个 8分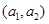 ,
,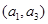 ,
,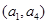 ,
,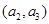 ,
, ,
,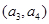 共6个 10分
共6个 10分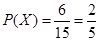 .故这2个都来自城市A的概率为
.故这2个都来自城市A的概率为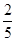 . 12分
. 12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
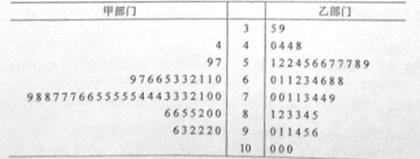
 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为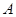 类工人),另外
类工人),另外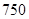 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按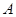 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).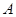 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?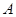 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.| 生产能力分组 |  |  |  |  |  |
| 人数 | 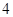 |  |  |  |  |
| 生产能力分组 |  |  |  |  |
| 人数 | 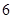 |  | 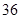 | 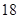 |


 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;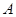 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.劳动生产率为1000元时,工资为130元 |
| B.劳动生产率平均提高1000元时,工资平均提高80元 |
| C.劳动生产率平均提高1000元时,工资平均提高130元 |
| D.当工资为250元时,劳动生产率为2000元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 运动员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
| | 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
| | 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 | [10,20) | [20,30) | [30,40] |
| 人数 | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
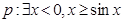 ,命题
,命题 :函数
:函数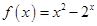 仅有两个零点,则命题
仅有两个零点,则命题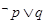 为真命题;
为真命题;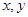 的一组观测数据
的一组观测数据 均在直线
均在直线 上,则
上,则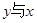 的线性相关系数
的线性相关系数 ;
;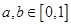 ,则使不等式
,则使不等式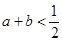 成立的概率是
成立的概率是 .
.| A.?? | B.?? | C.? | D.?? |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 |  |  |  |
| 男教师 |  |  | 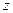 |
 、
、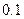 .
. 的值;
的值; 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 日期 | 1月 10日 | 2月 10日 | 3月 10日 | 4月 10日 | 5月 10日 | 6月 10日 |
| 昼夜温差 x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数 y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
 =
= x+
x+ .
. =
= =
= ,
, =
= -
-
 ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com