
 ,若
,若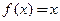 ,则称
,则称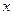 为
为 的“不动点”,若
的“不动点”,若 ,则称
,则称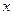 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为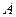 和
和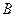 ,即
,即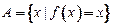 ,
, .
.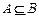 ;
; ,且
,且 ,求实数
,求实数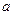 的取值范围;
的取值范围;  是
是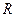 上的单调递增函数,
上的单调递增函数,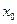 是函数的稳定点,问
是函数的稳定点,问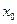 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.科目:高中数学 来源:不详 题型:解答题
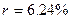 ,2000年该奖发放后基金总额约为21000万元。用
,2000年该奖发放后基金总额约为21000万元。用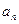
 表示为第
表示为第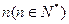 年该奖发放后的基金总额(2000年为第一年)。
年该奖发放后的基金总额(2000年为第一年)。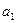 表示
表示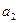 与
与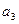 ,并根据所求结果归纳出
,并根据所求结果归纳出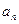 的表达式;
的表达式;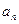 的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。
的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。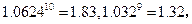
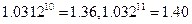 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
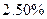 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为  【 】
【 】| A.11314元 | B.53877元 | C.11597元 | D.63877元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com