
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB=AC=AA1 , ![]() ,点D是BC的中点.
,点D是BC的中点.
(I)求证:AD⊥平面BCC1B1;
(II)求证:A1B∥平面ADC1;
(III)求二面角A﹣A1B﹣D的余弦值.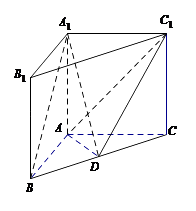
【答案】解:(I)因AB=AC,D为BC中点,故AD⊥BC 又因在直三棱柱A1B1C1﹣ABC中,CC1⊥平面ABC,故AD⊥CC1
又BC∩CC1=C,
故AD⊥平面BCC1B1
用向量方法证明本题请对应给分.
本题可分别以AB,AC,AA1为x,y,z轴建立空间直角坐标系,
也可分别以DC,DA,AD1(D1为棱B1C1中点)为x,y,z轴建立空间直角坐标系.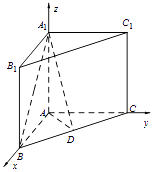
(II)如图,连接A1C∩AC1=E,连接DE.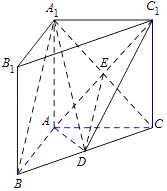
因D、E分别是BC、A1C的中点,故DE是△A1BC的中位线
故A1B∥DE(6分).因A1B平面ADC1
故A1B∥平面ADC1 .
用向量方法证明本题请如下给分:求出平面ADC1的法向量,
因A1B平面ADC1 ,
故A1B∥平面ADC1
(III)解法一:连接B1A∩BA1=O,分别取OB、AB中点H、O1 , 连接DH、DO1 . 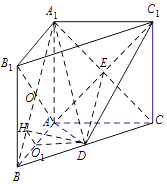
因为四边形ABB1A1是正方形且O1 , H分别是BA,BO中点,故HO1⊥AB.
又因O1 , H分别是BA,BC中点且AB⊥AC,故O1D⊥AB,
故∠O1HD就是二面角A﹣A1B﹣D的平面角.
设AB=2,则在Rt△HO1D中,∠HO1D=90°且 ![]() ,
,
故 ![]() ,故
,故 ![]() .
.
解法二:设AB=AC=2,则 ![]() ,故AB2+AC2=BC2 , 故AB⊥AC,
,故AB2+AC2=BC2 , 故AB⊥AC,
又因三棱柱A1B1C1﹣ABC为直三棱柱,故AB,AC,AA1两两垂直,故可建系如图.
则平面AA1B的法向量为 ![]() .
.
又 ![]() ,
,
设平面A1BD的法向量 ![]() ,
,
则 ![]() .
.
令z=1可得 ![]()
设所求二面角为θ,由图可知θ为锐角,故 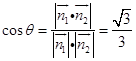
【解析】(Ⅰ)根据线面垂直的判定定理进行证明即可,(Ⅱ)根据线面平行的判定定理进行证明即可.(III)根据二面角的定义或者建立空间坐标系,求出平面的法向量,利用向量法进行求解即可.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A,B重合),点D,E分别是A在PC,PB上的射影,则( )
A.∠ACD是二面角A﹣PC﹣B的平面角
B.∠AED是二面角A﹣PB﹣C的平面角
C.∠EDA是二面角A﹣PC﹣B的平面角
D.∠DAE是二面角B﹣PA﹣C的平面角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a2=6,a3+a4=72.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an﹣n(n∈N*),求数列{bn}的前n项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x﹣1)f′(x)<0的解集为( ) 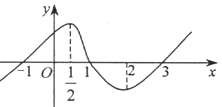
A.(﹣∞, ![]() )∪(1,2)
)∪(1,2)
B.(﹣1,1)∪(1,3)
C.(﹣1, ![]() )∪(3,+∞)
)∪(3,+∞)
D.(﹣∞,﹣1)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3 , a5﹣3b2=7.
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)在[﹣3,3]上是奇函数,且对任意x,y都有f(x+y)=f(x)+f(y),当x>0时,f(x)<0,f(1)=﹣2:
(Ⅰ)求f(2)的值;
(Ⅱ)判断f(x)的单调性,并证明你的结论;
(Ⅲ)求不等式f(x﹣1)>4的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com