
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左右焦点分别为F1 , F2 , 点P为椭圆C上的任意一点,若以F1 , F2 , P三点为顶点的三角形一定不可能为等腰钝角三角形,则椭圆C的离心率的取值范围是 .
的左右焦点分别为F1 , F2 , 点P为椭圆C上的任意一点,若以F1 , F2 , P三点为顶点的三角形一定不可能为等腰钝角三角形,则椭圆C的离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间![]() 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图(分组区间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并将分数从低到高分为四个等级:
),并将分数从低到高分为四个等级:
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
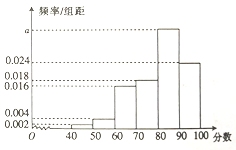
(1)求表中![]() 的值及不满意的人数;
的值及不满意的人数;
(2)在等级为不满意的师生中,老师占![]() ,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记
,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记![]() 为老师整改督导员的人数,求
为老师整改督导员的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=(a2﹣7a+6)+(a2﹣5a﹣6)i(a∈R)
(1)若复数z为纯虚数,求实数a的值;
(2)若复数z在复平面内的对应点在第四象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 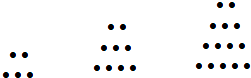
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象的纵坐标不变,横坐标缩短为原来的
的图象的纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象.已知函数
的图象.已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)设函数![]() ,证明:对任意
,证明:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com