
【题目】已知函数![]()
(1)判断![]() 的奇偶性并证明;
的奇偶性并证明;
(2)判断![]() 的单调性并说明理由;
的单调性并说明理由;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)奇函数,证明见解析;(2)增函数,理由见解析;(3)![]()
【解析】
(1)求出![]() 的定义域,再计算
的定义域,再计算![]() 与
与![]() 比较,即可判断奇偶性;
比较,即可判断奇偶性;
(2)对函数求导,判断导函数大于![]() ,即可的
,即可的![]() 的单调性;
的单调性;
(3)利用函数的奇偶性和单调性和将![]() 转化为
转化为![]() ,再分情况讨论即可得出
,再分情况讨论即可得出![]() 的取值范围.
的取值范围.
解(1)判断:![]() 是奇函数.
是奇函数.
证明:因为![]() ,定义域为
,定义域为![]() ,
,
![]()
所以![]() 是奇函数;
是奇函数;
(2)判断:![]() 在
在![]() 上是增函数.
上是增函数.
证明:因为![]()
所以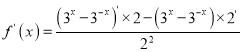
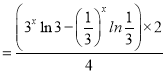
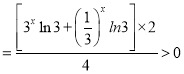
所以![]() 在
在![]() 上是增函数.
上是增函数.
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
因为![]() 所以
所以![]() ,
,
由(1)知![]() 是奇函数,则
是奇函数,则![]()
又由(2)知![]() 在
在![]() 上是增函数,则
上是增函数,则![]()
![]() ,对任意
,对任意![]() 恒成立,
恒成立,
①当![]() 时,
时,![]() ,符合题意;
,符合题意;
②当![]() 时,
时,![]() ,
,
因为![]() ,无最小值,所以不合题意;
,无最小值,所以不合题意;
③当![]() 时,
时,![]() ,
,
则![]() ,解得
,解得![]() ,所以
,所以![]() ,符合题意;
,符合题意;
综上所述:![]() .
.
故若![]() 对任意
对任意![]() 恒成立,
恒成立,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐.下表是西南地区某大学近五年的录取平均分与省一本线对比表:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
省一本线 |
|
|
|
|
|
录取平均分 |
|
|
|
|
|
录取平均分与省一本线分差 |
|
|
|
|
|
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的性回归方程;
的性回归方程;
(2)假设2019年该省一本线为![]() 分,利用(1)中求出的回归方程预测2019年该大学录取平均分.
分,利用(1)中求出的回归方程预测2019年该大学录取平均分.
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ;
;
(1)若函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]() ,若存在,求出
,若存在,求出![]() ,
,![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中美贸易争端一直不断,2003年至2005年末,由美国单方面挑起的一系列贸易摩擦给中美贸易关系蒙上了浓重的阴影,贸易大战似乎一触即发,中美两国进入了前所未有的贸易摩擦期.2018年,特朗普政府不顾中方劝阻,执意发动贸易战,掀起了又一轮的中美贸易争端.我国某种出口商品定价为每件60美元,美国不加收关税时每年大约出口80万件,中美经贸摩擦后,美国政府执意要加收进口关税,每进口100美元商品要征税P美元,因此每年出口量将减少![]() 万件.
万件.
(1)如果美国政府计划每年对该商品加征的关税金额不少于128万美元,那么税率应怎样确定?
(2)在美国政府计划每年对该商品加征关税金额不少于128万美元的前提下,如何确定税率,才会使得我国生产该商品的厂家税后获取最大的出口额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某煤炭公司销售人员根据该公司以往的销售情况,得到如下频率分布表
日销售量分组 | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
频率 | 0.10 | 0.20 | 0.30 | 0.25 | 0.15 |
(1)在下图中作出这些数据的频率分布直方图;

(2)将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.若未来3天内日销售量不低于6吨的天数为X,求X的分布列、数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
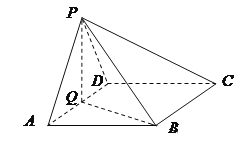
【题目】如图,四棱锥![]() 中,底面ABCD为菱形,
中,底面ABCD为菱形,![]() ,Q是AD的中点.
,Q是AD的中点.
(Ⅰ)若![]() ,求证:平面PQB
,求证:平面PQB![]() 平面PAD;
平面PAD;
(Ⅱ)若平面APD![]() 平面ABCD,且
平面ABCD,且![]() ,点M在线段PC上,试确定点M的位置,使二面角
,点M在线段PC上,试确定点M的位置,使二面角![]() 的大小为
的大小为![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com