
 17、如图是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.
17、如图是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:2010-2011学年陕西省西安市高三第三次质量检测理科数学 题型:解答题
((本小题满分12分)
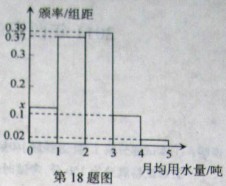
如图是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.(1)求直方图中x的值;(2)若将频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样).求月均用水量在3至4吨的居民数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年内蒙古包头33中高二(上)期中数学试卷Ⅱ(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年湖南省高考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年高考数学试卷精编:11.2 随机变量(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com