
分析 先求出数列$\left\{{{{({\frac{2}{3}})}^n},n∈N*}\right\}$前n项和,再求出前n项和的极限,从而求出结果.
解答 解:数列$\left\{{{{({\frac{2}{3}})}^n},n∈N*}\right\}$前n项和:
Sn=$\frac{\frac{2}{3}[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$=2[1-($\frac{2}{3}$)n],
∴数列$\left\{{{{({\frac{2}{3}})}^n},n∈N*}\right\}$所有项的和为:
S=$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}2[1-(\frac{2}{3})^{n}]$=2.
故答案为:2.
点评 本题考查等比数列的前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
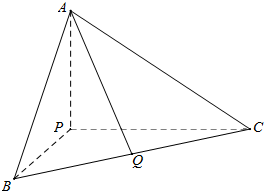 在三棱锥P-ABC中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥P-ABC的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示).
在三棱锥P-ABC中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥P-ABC的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
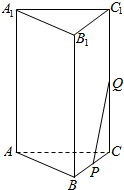 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两个平面的法向量所成的角是这两个平面所成的角 | |
| B. | 设空间向量$\overrightarrow a$,$\overrightarrow b$为非零向量,若$\overrightarrow a•\overrightarrow b>0$,则$<\overrightarrow a,\overrightarrow b>$为锐角 | |
| C. | 方程mx2+ny2=1(m>0,n>0)表示的曲线是椭圆 | |
| D. | 等轴双曲线的渐近线互相垂直,离心率等于$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com