Question

现有甲乙两船，其中甲船在某岛B的正南方A处，A与B相距7公里，甲船自A处以4公里/小时的速度向北方向航行，同时乙船以6公里/小时的速度自B岛出发，向北60°西方向航行，问    分钟后两船相距最近．

Answer 1

【答案】分析：设经过x小时距离最小，然后分别表示出甲乙距离B岛的距离，再由余弦定理表示出两船的距离，最后根据二次函数求最值的方法可得到答案．
解答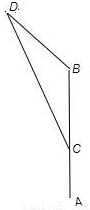：解：假设经过x小时两船相距最近，甲乙分别行至C，D如图示
可知BC=7-4x，BD=6x，∠CBD=120°
CD²=BC²+BD²-2BC×BD×cosCBD=（7-4x）²+36x²+2×（7-4x）×6x×
=28x²-28x+49，
当x=小时即 30分钟时距离最小
故答案为：30．
点评：本题主要考查已知三角函数模型的应用问题、余弦定理的应用，关键在于画出图象．属基础题．