【题目】现有10道题，其中6道甲类题，4道乙类题，小明同学从中任取3道题解答．
（Ⅰ）求小明同学至少取到1道乙类题的概率；
（Ⅱ）已知所取的3道题中有2道甲类题，1道乙类题．若小明同学答对每道甲类题的概率都是
，答对每道乙类题的概率都是
，且各题答对与否相互独立．求小明同学至少答对2道题的概率．
互动课堂系列答案
激活思维智能训练课时导学练系列答案科目：高中数学 来源： 题型：
【题目】如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．
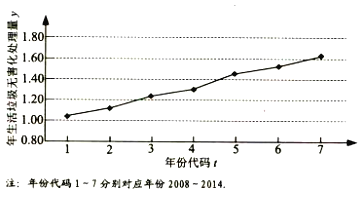
（Ⅰ）由折线图看出，可用线性回归模型拟合
与
的关系，请用相关系数加以说明；
（Ⅱ）建立
关于
的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
参考数据： 
， 
， 
， 
．
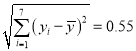参考公式：相关系数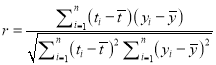
，
回归方程
， 
，
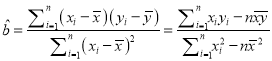本题中斜率和截距的最小二乘估计公式分别为：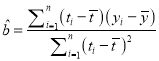 
， 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
若
，过点
的直线
交曲线
于
两点，且
，求直线
的方程；
若曲线
表示圆，且直线
与圆
交于
两点，是否存在实数
，使得以
为直径的圆过原点，若存在，求出实数
的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
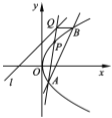
【题目】已知直线
的方程为
，点
是抛物线
上到直线
距离最小的点，点
是抛物线上异于点
的点，直线
与直线
交于点
，过点
与
轴平行的直线与抛物线
交于点
.
（Ⅰ）求点
的坐标；
（Ⅱ）证明直线
恒过定点，并求这个定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某地区某种农产品的年产量
（单位：吨）对价格
（单位：千元/吨）和利润
的影响，对近五年该农产品的年产量和价格统计如下表：
（1）求
关于
的线性回归方程；
（2）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润
取到最大值？（结果保留两位小数）
参考公式：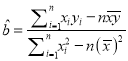 
， 
参考数据： 
， 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设甲、乙、丙三个乒乓球协会的运动员人数分别为27，9，18，先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛．
（Ⅰ）求应从这三个协会中分别抽取的运动员人数；
（Ⅱ）将抽取的6名运动员进行编号，编号分别为
，从这6名运动员中随机抽取2名参加双打比赛．
（ⅰ）用所给编号列出所有可能的结果；
（ⅱ）设
为事件“编号为
的两名运动员至少有一人被抽到”，求事件
发生的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为
（1）求频率分布图中
的值，并估计该企业的职工对该部门评分不低于80的概率；
（2）从评分在
的受访职工中，随机抽取2人，求此2人评分都在
的概率．．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解学生身高情况，某校以
的比例对全校1000名学生按性别进行分层抽样调查，已知男女比例为
，测得男生身高情况的频率分布直方图（如图所示）：
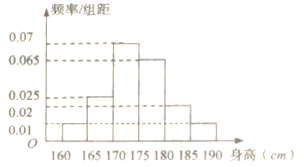
（1）计算所抽取的男生人数，并估计男生身高的中位数（保留两位小数）；
（2）从样本中身高在
之间的男生中任选2人，求至少有1人身高在
之间的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
