
【题目】国内某汽车品牌一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如下:
的概率分布如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)若每个月被消费者投诉的次数互不影响,求该汽车品牌在五个月内被消费者投诉3次的概率.
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
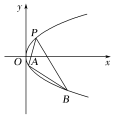
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司今年年初用98万元购进一艘渔船用于捕捞,第一年需要各种费用12万元.从第二年起包括维修费在内每年所需费用比上一年增加4万元.该船每年捕捞总收入50万元.
(1)问捕捞几年后总盈利最大,最大是多少?
(2)问捕捞几年后的平均利润最大,最大是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 满足以下4个条件.
满足以下4个条件.
①函数![]() 的定义域是
的定义域是![]() ,且其图象是一条连续不断的曲线;
,且其图象是一条连续不断的曲线;
②函数![]() 在
在![]() 不是单调函数;
不是单调函数;
③函数![]() 是偶函数;
是偶函数;
④函数![]() 恰有2个零点.
恰有2个零点.
(1)写出函数![]() 的一个解析式;
的一个解析式;
(2)画出所写函数![]() 的解析式的简图;
的解析式的简图;
(3)证明![]() 满足结论③及④.
满足结论③及④.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机企业为确定下一年度投入某种产品的研发费用,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 千万元与年销售量
千万元与年销售量![]() 千万件的数据,得到散点图1,对数据作出如下处理:令
千万件的数据,得到散点图1,对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如图2:
,得到相关统计量的值如图2:

(1)利用散点图判断![]() 和
和![]()
![]() 哪一个更适合作为年研发费用
哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归类型(不必说明理由),并根据数据,求出
的回归类型(不必说明理由),并根据数据,求出![]() 与
与![]() 的回归方程;
的回归方程;
(2)已知企业年利润![]() 千万元与
千万元与![]() 的关系式为
的关系式为![]() (其中
(其中![]() 为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在坐标平面上,纵横坐标都是整数的点称为整点.试证:存在一个同心圆的集合,使得:(1)每个整点都在此集体的某一圆周上;(2)此集合的每个圆周上.有且只有一个整点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com