函数
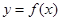
是定义在
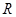
上的增函数,函数
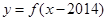
的图象关于点
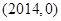
对称.若实数
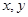
满足不等式
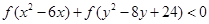
,则
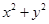
的取值范围是 ( )
试题分析:函数
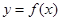
是定义在
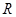
上,易知函数
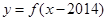
的图像是函数
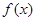
的图像向右平移了2014个单位,因为函数
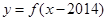
的图象关于点
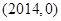
对称,所以函数
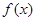
的图像关于点(0,0)对称,即函数
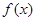
是奇函数.由不等式
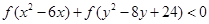
得
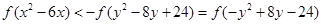
.又函数
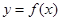
是定义在
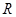
上的增函数,所以
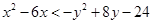
,即
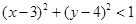
,设点
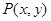
,由
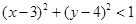
知点
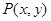
在以(3,4)为圆心,1为半径的圆内.
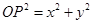
(
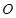
为原点),因为易知圆心到原点的距离为5,所以
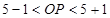
,所以
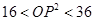
,即
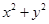
的取值范围是(16,36).
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设函数
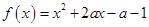
,
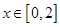
,
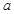
为常数
(1)求
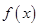
的最小值
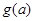
的解析式;
(2)在(1)中,是否存在最小的整数
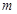
,使得
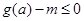
对于任意
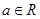
均成立,若存在,求出
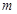
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
试判断函数
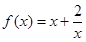
在[
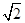
,+∞)上的单调性.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
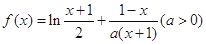
.
(Ⅰ) 若函数
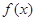
在
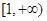
上为增函数, 求实数
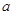
的取值范围;
(Ⅱ) 求证:当
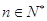
且
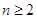
时,
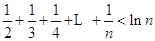
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
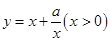
有如下性质:若常数
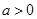
,则函数在
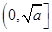
上是减函数,在
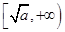
上是增函数。已知函数
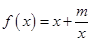
(
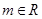
为常数),当
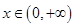
时,若对任意
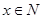
,都有
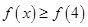
,则实数
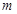
的取值范围是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
定义在
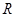
上的函数
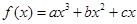
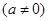
的单调增区间为
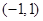
,若方程
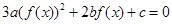
恰有6个不同的实根,则实数
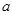
的取值范围是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设
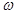
>0,若函数
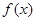
=sin
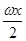
cos
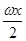
在区间[-
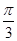
,
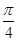
]上单调递增,则
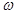
的范围是_____________.
查看答案和解析>>

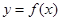 是定义在
是定义在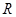 上的增函数,函数
上的增函数,函数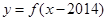 的图象关于点
的图象关于点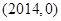 对称.若实数
对称.若实数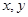 满足不等式
满足不等式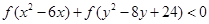 ,则
,则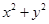 的取值范围是 ( )
的取值范围是 ( )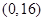
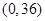
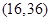
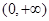
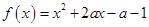 ,
,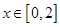 ,
,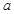 为常数
为常数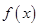 的最小值
的最小值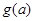 的解析式;
的解析式;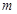 ,使得
,使得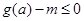 对于任意
对于任意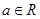 均成立,若存在,求出
均成立,若存在,求出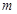 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.