【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中，AC∩BD=O，E是线段B1C（含端点）上的一动点，则
①OE⊥BD1；
②OE
面A1C1D；
③三棱锥A1﹣BDE的体积不是定值；
④OE与A1C1所成的最大角为90°．
上述命题中正确的个数是（ ）
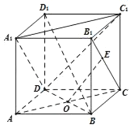
A.1B.2C.3D.4
科目：高中数学 来源： 题型：
【题目】正四棱锥
的底面正方形边长是3，
是在底面上的射影，
，
是
上的一点，过且与
、
都平行的截面为五边形
．
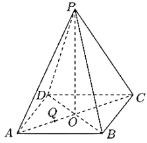
（1）在图中作出截面，并写出作图过程；
（2）求该截面面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在
中，
，
，
，
分别为
，
的中点
是由
绕直线
旋转得到，连结
，
，
.
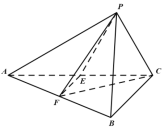
（1）证明：
平面
；
（2）若
，棱
上是否存在一点
，使得
？若存在，确定点 的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设有下列四个命题：
p1：两两相交且不过同一点的三条直线必在同一平面内.
p2：过空间中任意三点有且仅有一个平面.
p3：若空间两条直线不相交，则这两条直线平行.
p4：若直线l
平面α，直线m⊥平面α，则m⊥l.
则下述命题中所有真命题的序号是__________.
①
②
③
④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加.为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据(xi，yi)(i=1，2，…，20)，其中xi和yi分别表示第i个样区的植物覆盖面积(单位：公顷)和这种野生动物的数量，并计算得
，
，
，
，
.
（1）求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；
（2）求样本(xi，yi)(i=1，2，…，20)的相关系数（精确到0.01）；
（3）根据现有统计资料，各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.
附：相关系数r=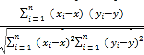
，
≈1.414.
查看答案和解析>>
科目：高中数学 来源： 题型：
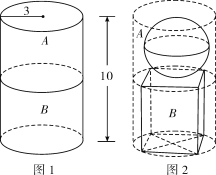
【题目】石雕工艺承载着几千年的中国石雕文化，随着科技的发展，机器雕刻产品越来越多．某石雕厂计划利用一个圆柱形的石材（如图1）雕刻制作一件工艺品（如图2），该作品的上方是一个球体，下方是一个正四棱柱，经测量，圆柱形石材的底面半径
米，高
米，制作要求如下：首先需将石材切割为体积相等的两部分（分别称为圆柱A和圆柱B），要求切面与原石材的上、下底面平行（不考虑损耗），然后将圆柱A切割打磨为一个球体，将圆柱B切割打磨为一个长方体，则加工打磨后所得工艺品的体积的最大值为________立方米.
查看答案和解析>>
科目：高中数学 来源： 题型：
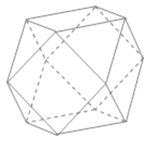
【题目】半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美．如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，它们的棱长都相等，其中八个为正三角形，六个为正方形，称这样的半正多面体为二十四等边体．若二十四等边体的棱长为2，则其体积为______；若其各个顶点都在同一个球面上，则该球的表面积为______．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)
（a＞0）．
（1）证明：当x∈[1，+∞）时，f(x)≥1．
（2）当0<a≤1时，对于任意的x∈(0，+∞)，f(x)≥m，求整数m的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
