
| A. | $(-∞,\frac{1}{4}]$ | B. | $(-\frac{3}{4},+∞)$ | C. | $[-\frac{3}{4},\frac{1}{4}]$ | D. | $(-1,\frac{1}{4}]$ |
分析 x0为函数f(x)的“不动点”,则方程f(x)=x,即ax2+1-x=0有实根,故△=1+4a≥0,得出a的范围,
由方程f(f(x))=x,化为:(ax2+1)2+1=x,即(ax2+1)2-x2+x2+a=x,利用平方差公式分解因式得,(x2+a-x)(x2+x+a+1)=0,由函数f(x)=x2+a(a∈R)的“稳定点”恰是它的“不动点”,得方程x2+x+a+1=0无实数根,再解出a的范围.
解答 解:x0为函数f(x)的“不动点”,则方程f(x)=x,即ax2+1-x=0有实根,故△=1-4a≥0,∴a$≤\frac{1}{4}$,
如果“稳定点”恰是它的“不动点”,则上述方程的根x0为方程f(f(x))=x,即ax2+1=x的实根,
方程f(f(x))=x可化为:a(ax2+1)2+1=x,即a(ax2+1)2-ax2+ax2+1=x,利用平方差公式分解因式得,
∴a(ax2+1+x)(ax2+1-x)+(x2+a-x)=0,∴a(x2+a-x)(x2+x+a+1)=0,
∵函数f(x)=ax2+1(a∈R)的“稳定点”恰是它的“不动点”,∴方程x2+x+a+1=0无实数根,
∴1-4(a+1)<0,∴$a>-\frac{3}{4}$,
综上,$\frac{1}{4}≥a>-\frac{3}{4}$,
故选:C.
点评 本题考查对新概念的理解和运用的能力,同时考查了二次方程根的相关知识.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
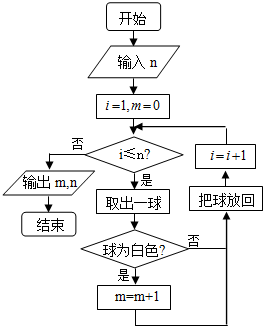
| n | 100 | 150 | 200 | 500 | 800 | 1000 |
| m | 58 | 96 | 116 | 295 | 484 | 601 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com