Question

甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等.而两个保护区每个季度发现违反保护条例的事件次数的分布列分别为:

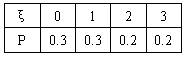
甲保护区:

X1	0	1	2	3
P	0.3	0.3	0.2	0.2

乙保护区:

X2	0	1	2
P	0.1	0.5	0.4

试评价这两个保护区的管理水平.

Answer 1

分析：数学期望仅体现了随机变量取值的平均大小,但有时仅知道均值大小还是不够的,比如:两个随机变量的均值相等了(即数学期望值相等),这就还需要知道随机变量的取值如何在均值周围变化,即计算其方差(或是标准差).方差大说明随机变量取值分散性大;方差小说明取值分散性小,或者说取值比较集中、稳定.

一是要比较一下甲、乙两个保护区内每季度发生的违规事件次数的均值,即数学期望;二是要看发生违规事件的波动情况,即方差值的大小(当然,亦可计算其标准差,同样说明道理).

解：甲保护区的违规次数X₁的数学期望和方差为:

EX₁=0×0.3+1×0.3+2×0.2+3×0.2=1.3;

DX₁=(0-1.3)²×0.3+(1-1.3)²×0.3+(2-1.3)²×0.2+(3-1.3)²×0.2=1.21.

乙保护区的违规次数X₂的数学期望和方差为：

EX₂=0×0.1+1×0.5+2×0.4=1.3;

DX₂=(0-1.3)²×0.1+(1-1.3)²×0.5+(2-1.3)²×0.4=0.41.

因为EX₁=EX₂，DX₁＞DX₂,所以两个保护区内每季度发生的违规平均次数是相同的,但乙保护区内的违规事件次数更集中和稳定,而甲保护区的违规事件次数相对分散,波动性较大.

绿色通道:期望决定了随机变量的取值的平均水平、集中位置，而方差求的是随机变量的稳定与波动情况.要防止只由期望来评价两者稳定性,而应该进一步考查其方差.