
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
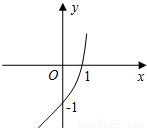
 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,数列{an}的前n项的和Sn=an+1+b、Tn为数列{bn}的前n项的和.且Tn=
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,数列{an}的前n项的和Sn=an+1+b、Tn为数列{bn}的前n项的和.且Tn=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| x\~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2\~(-1)(3)(-2)(1) |
| 1 |
| 1-ak |
. |
| 2\~(a1)(a2)(a3)…(a3n-2)(a3n-1)(a3n) |
. | ||||||||||
t\~(
|
| lim |
| n→∞ |
| dn |
| dn+1 |
查看答案和解析>>
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学理 题型:044
如图,曲线y=![]() 上的点Pi(
上的点Pi(![]() ,ti)(i=1,2,…,n,…)与x轴正半轴上的点Qi及原点O构成一系列正三角形PiQi-1Qi(Q0与O重合),记an=|QnQn-1|.
,ti)(i=1,2,…,n,…)与x轴正半轴上的点Qi及原点O构成一系列正三角形PiQi-1Qi(Q0与O重合),记an=|QnQn-1|.
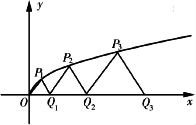
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式an;
(Ⅲ)设Sn为数列{an}的前n项和;若对于任意的实数λ∈[0,1],总存在自然数k,当n≥k时,3Sn-3n+2≥(1-λ)(3an-1)恒成立,求k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
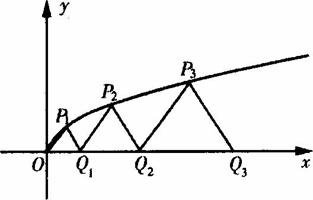
(Ⅰ)求a1的值;
(Ⅱ)求数列{an}的通项公式an;
(Ⅲ)设Sn为数列{an}的前n项和;若对于任意的实数λ∈[0,1],总存在自然数k,当n≥k时,3Sn-3n+2≥(1—λ)(3an-1)恒成立,求k的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省宿迁市高考数学模拟试卷(二)(解析版) 题型:解答题
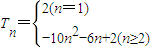
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com