练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某班制定了数学学习方案：星期一和星期日分别解决个数学问题，且从星期二开始，每天所解决问题的个数与前一天相比，要么“多一个”要么“持平”要么“少一个”，则在一周中每天所解决问题个数的不同方案共有（ ）

    A. 种 B. 种 C. 种 D. 种

    【答案】A

    【解析】分析：因为星期一和星期日分别解决4个数学问题，所以从这周的第二天开始后六天中“多一个”或“少一个”的天数必须相同，都是0、1、2、3天，共四种情况，利用组合知识可得结论．

    详解：因为星期一和星期日分别解决4个数学问题，所以从这周的第二天开始后六天中“多一个”或“少一个”的天数必须相同，

    所以后面六天中解决问题个数“多一个”或“少一个”的天数可能是0、1、2、3天，共四种情况，

    所以共有=141种．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 ． （I）求函数f（x）的最小正周期和最小值；
    （II）在△ABC中，A，B，C的对边分别为a，b，c，已知 ，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的一系列对应值如下表：

    -2

    4

    -2

    4

    （1）根据表格提供的数据求函数的解析式；

    （2）求函数的单调递增区间和对称中心；

    （3）若当时，方程 恰有两个不同的解，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线(b>0)的左、右焦点分别为，其一条渐近线方程为y=x，点P在该双曲线上，且，则=（ ）

    A. 4 B. 4 C. 8 D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，PA⊥平面ABCD，CD⊥AD，BC∥AD，.

    （Ⅰ）求证：CD⊥PD；

    （Ⅱ）求证：BD⊥平面PAB；

    （Ⅲ）在棱PD上是否存在点M，使CM∥平面PAB，若存在，确定点M的位置，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    如图在直三棱柱ABC—A1B1C1中，AC=3，BC=4，AB=5，AA1=4,点D是AB的

    中点.

    (1) 求证： AC⊥BC1

    (2) 求证：AC1∥平面CDB1

    (3) 求异面直线AC1与B1C所成角的余弦值.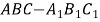

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某理科考生参加自主招生面试，从道题中（道甲组题和道乙组题）不放回地依次任取道作答.

    （1）求该考生在第一次抽到甲组题的条件下，第二次和第三次均抽到乙组题的概率；

    （2）规定理科考生需作答道甲组题和道乙组题，该考生答对甲组题的概率均为，答对乙组题的概率均为，若每题答对得，否则得零分.现该生已抽到道题（道甲组题和道乙组题），求其所得总分的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣m（x+1）ln（x+1）（m＞0）的最大值是0，函数g（x）=x﹣a（x2+2x）（a∈R）． （Ⅰ）求实数m的值；
    （Ⅱ）若当x≥0时，不等式f（x）≥g（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 在（t，10﹣t2）上有最大值，则实数t的取值范围为（ ）
    A.
    B.
    C.[﹣2，1）
    D.（﹣2，1）

    查看答案和解析>>

    同步练习册答案