
【题目】已知函数 ![]() 的定义域为集合A,y=﹣x2+2x+2a的值域为B.
的定义域为集合A,y=﹣x2+2x+2a的值域为B.
(1)若a=2,求A∩B
(2)若A∪B=R,求实数a的取值范围.
【答案】
(1)解:依题意:整理得A={x︳x>3},函数y=﹣x2+2x+2a=﹣(x﹣1)2+1+2a≤1+2a,即B={x︳x≤2a+1},
当a=2时,B={x|x≤5},
∴A∩B={x︳3<x≤5}
(2)解:∵A∪B=R,∴根据题意得:2a+1≥3,
解得:a≥1,
则实数a的取值范围是[1,+∞)
【解析】求出函数y= ![]() 的定义域确定出A,求出y=﹣x2+2x+2a的值域确定出B,(1)把a=2代入确定出B,求出A与B的交集即可;(2)由A与B的并集为R,列出关于a的不等式,求出不等式的解集即可得到a的范围.
的定义域确定出A,求出y=﹣x2+2x+2a的值域确定出B,(1)把a=2代入确定出B,求出A与B的交集即可;(2)由A与B的并集为R,列出关于a的不等式,求出不等式的解集即可得到a的范围.
【考点精析】根据题目的已知条件,利用集合的并集运算和集合的交集运算的相关知识可以得到问题的答案,需要掌握并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立;交集的性质:(1)A∩B
B,反之也成立;交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】某企业生产的新产品必须先靠广告打开销路,该产品广告效应y(单位:元)是产品的销售额与广告费x(单位:元)之间的差,如果销售额与广告费x的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元. (Ⅰ)求出广告效应y与广告费x之间的函数关系式;
(Ⅱ)该企业投入多少广告费才能获得最大的广告效应?是不是广告费投入越多越好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
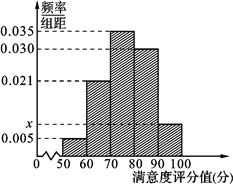
(1) 求图中![]() 的值;
的值;
(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在区间(0,+∞)上的增函数,f(2)=1,且对于任意a,b∈(0,+∞), ![]() 恒成立. (I)求f(8);
恒成立. (I)求f(8);
(II)求不等式 ![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);
表示相应事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
①从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在[﹣2,2]上的奇函数f(x)=x5+x3+b
(1)求b值;
(2)若f(x)在[0,2]上单调递增,且f(m)+f(m﹣1)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,动点
,动点![]() 满足
满足![]() .设动点
.设动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求动点![]() 的轨迹方程,并说明轨迹
的轨迹方程,并说明轨迹![]() 是什么图形;
是什么图形;
(2)求动点![]() 与定点
与定点![]() 连线的斜率的最小值;
连线的斜率的最小值;
(3)设直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,是否存在以线段
两点,是否存在以线段![]() 为直径的圆经过
为直径的圆经过![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com