
【题目】已知 ![]() 是R上的增函数,则a的取值范围是 .
是R上的增函数,则a的取值范围是 .
【答案】[2,+∞)
【解析】解:首先,y=logax在区间[1,+∞)上是增函数
且函数y=(a+2)x﹣2a区间(﹣∞,1)上也是增函数
∴a>1…(1)
其次在x=1处函数对应的第一个表达式的值要小于或等于第二个表达式的值,即
(a+2)﹣2a≤loga1a≥2…(2)
联解(1)、(2)得a≥2.
所以答案是:[2,+∞).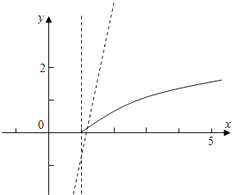
【考点精析】解答此题的关键在于理解函数单调性的性质的相关知识,掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集,以及对对数函数的单调性与特殊点的理解,了解过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数.


科目:高中数学 来源: 题型:
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 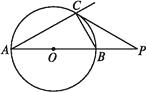
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D,E,F分别为△ABC的边BC,CA,AB的中点,记 ![]() =a ,
=a , ![]() =b.则下列命题中正确的个数是( )
=b.则下列命题中正确的个数是( )
① ![]() =
= ![]() a-b;②
a-b;② ![]() =a+
=a+ ![]() b;③
b;③ ![]() =
= ![]() a+
a+ ![]() b;④
b;④ ![]() 0.
0.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+3x+a
(1)当a=﹣2时,求不等式f(x)>2的解集
(2)若对任意的x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(1)求f(0)的值和实数m的值;
(2)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率.
(Ⅰ)取到的2只都是次品;
(Ⅱ)取到的2只中恰有一只次品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com