
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
分析 令g(x)=$\frac{f(x)}{x}$,则g(x)周期为1,计算f($\frac{1}{2}$)和f(0),根据周期得出f($\frac{5}{2}$),从而得出答案.
解答 解:令x=-$\frac{1}{2}$得-$\frac{1}{2}$f($\frac{1}{2}$)=$\frac{1}{2}$f(-$\frac{1}{2}$)=$\frac{1}{2}$f($\frac{1}{2}$),
∴f($\frac{1}{2}$)=0,
令x=0得f(0)=0,
∵xf(x+1)=(x+1)f(x),∴$\frac{f(x+1)}{x+1}=\frac{f(x)}{x}$.
令g(x)=$\frac{f(x)}{x}$,则g(x+1)=g(x),
∴g(x)的周期为1,
∴g($\frac{5}{2}$)=g($\frac{1}{2}$)=$\frac{f(\frac{1}{2})}{\frac{1}{2}}$=0,
即g($\frac{5}{2}$)=$\frac{f(\frac{5}{2})}{\frac{5}{2}}$=0,∴f($\frac{5}{2}$)=0,
∴f(f($\frac{5}{2}$))=f(0)=0.
故选A.
点评 本题考查了抽象函数的周期,构造函数g(x)是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
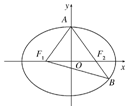 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{27}{5},+∞)$ | B. | (-3,+∞) | C. | $(-2\sqrt{2},+∞)$ | D. | $(-3,-2\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{3}^{9}}{{2}^{10}}$ | B. | -$\frac{{3}^{10}}{{2}^{10}}$ | C. | $\frac{{3}^{9}}{{2}^{10}}$ | D. | $\frac{{3}^{10}}{{2}^{10}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}i$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{2}i$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com