练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】写出求过两点M(-2，-1)，N(2，3)的直线与坐标轴围成面积的一个算法.

    【答案】见解析

    【解析】试题分析：过两个点的直线与两个坐标轴所围成的三角形的面积，设计算法时首先要输入这两个点的坐标，根据这两个点的坐标才能写出直线的两点式方程，然后分别设计两步求直线与两个坐标轴的交点，得出直线与x轴交点的横坐标及直线与y轴交点的纵坐标，最后一步设计求出三角形的面积，输出面积的值.

    试题解析：

    第一步：取x1=-2，y1=-1，x2=2，y2=3；

    第二步：计算=；

    第三步：在第二步结果中令x=0得到y的值m，得直线与y轴交点(0，m)；

    第四步：在第二步结果中令y=0得到x的值n，得直线与x轴交点(n，0)；

    第五步：计算S=|m|·|n|；

    第六步：输出运算结果.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （1）当时，求的最小值；

    （2）存在时，使得不等式成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着手机的发展，“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查，随机抽取了50人，他们年龄的频数分布及对“使用微信交流”赞成人数如下表.

    年龄（单位：岁）

    [15,25）

    [25,35）

    [35,45）

    [45,55）

    [55,65）

    [65,75）

    频数

    5

    10

    15

    10

    5

    5

    赞成人数

    5

    10

    12

    7

    2

    1

    （Ⅰ）若以“年龄45岁为分界点”，由以上统计数据完成下面列联表，并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关；

    年龄不低于45岁的人数

    年龄低于45岁的人数

    合计

    赞成

    不赞成

    合计

    （Ⅱ）若从年龄在[25,35）和[55,65）的被调查人中按照分层抽样的方法选取6人进行追踪调查，并给予其中3人“红包”奖励，求3人中至少有1人年龄在[55,65）的概率.

    参考数据如下：

    附临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    的观测值： （其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来空气质量逐步恶化，雾霾天气现象增多，大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关，在市第一人民医院随机对入院50人进行了问卷调查，得到如下的列联表：

    患心肺疾病

    不患心肺疾病

    合计

    男

    20

    5

    25

    女

    10

    15

    25

    合计

    30

    20

    50

    （1）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；

    （2）已知在患心肺疾病的10位女性中，有3位又患有胃病，现在从患心肺疾病的10位女性中，选出3位进行其他方面的排查，其中患胃病的人数为，求的分布列、数学期望.

    参考公式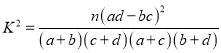： ，其中.

    下面的临界值仅供参考：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,在区间内任取两个实数,且,若不等式恒成立,则实数的取值范围为( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市从现有甲、乙两种酸奶的日销售量（单位：箱）的1200个数据（数据均在区间内）中，按照5%的比例进行分层抽样，统计结果按， ， ， ， 分组，整理如下图：

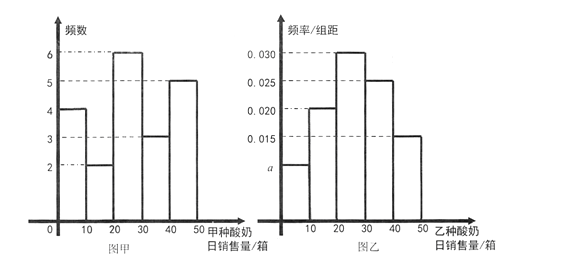
    （Ⅰ）写出频率分布直方图（图乙）中的值；记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为， ，试比较与的大小（只需写出结论）；

    （Ⅱ）从甲种酸奶日销售量在区间的数据样本中抽取3个，记在内的数据个数为，求的分布列；

    （Ⅲ）估计1200个日销售量数据中，数据在区间中的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）过原点作曲线的切线，求切线方程；

    （Ⅱ）当时，讨论曲线与曲线公共点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

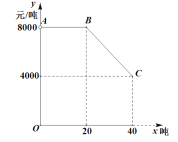
    【题目】乔经理到老陈的果园里一次性采购一种水果，他俩商定：乔经理的采购价（元/吨）与采购量（吨）之间函数关系的图像如图中的折线段所示（不包含端点但包含端点）.

    （1）求与之间的函数关系式；

    （2）已知老陈种植水果的成本是2800元/吨，那么乔经理的采购量为多少时，老陈在这次买卖中所获的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年五一假期期间，高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査，将他们在某段高速公路的车速分成六段： 后得到如图的频率分布直方图.

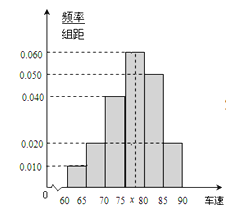
    （Ⅰ）求这40辆小型车辆车速的众数和中位数以及平均数的估计值.

    （Ⅱ）若从车速在的车辆中任抽取2辆，求车速在的车辆恰有一辆的概率.

    查看答案和解析>>

    同步练习册答案