
【题目】已知![]() 是由具有公共直角边的两块直角三角板(
是由具有公共直角边的两块直角三角板(![]() 与
与![]() )组成的三角形,如左下图所示.其中,
)组成的三角形,如左下图所示.其中,![]() .现将
.现将![]() 沿斜边
沿斜边![]() 进行翻折成
进行翻折成![]() (
(![]() 不在平面
不在平面![]() 上).若
上).若![]() 分别为
分别为![]() 和
和![]() 的中点,则在
的中点,则在![]() 翻折过程中,下列命题不正确的是( )
翻折过程中,下列命题不正确的是( )

A. 在线段![]() 上存在一定点
上存在一定点![]() ,使得
,使得![]() 的长度是定值
的长度是定值
B. 点![]() 在某个球面上运动
在某个球面上运动
C. 存在某个位置,使得直线![]() 与
与![]() 所成角为
所成角为![]()
D. 对于任意位置,二面角![]() 始终大于二面角
始终大于二面角![]()
【答案】C
【解析】分析:由题意,可的二面角![]() 和二面角
和二面角![]() 由共同的平面角
由共同的平面角![]() ,
,
且另一个面都过点![]() ,过点
,过点![]() 作平面
作平面![]() 的垂线,即可得到二面角
的垂线,即可得到二面角![]() 和二面角
和二面角![]() 的平面角,进而的大小关系即可.
的平面角,进而的大小关系即可.
详解:不妨设![]() ,取
,取![]() 中点
中点![]() ,易知
,易知![]() 落在线段
落在线段![]() 上,且
上,且![]() ,
,
所以点![]() 到点
到点![]() 的距离始终为
的距离始终为![]() ,即点
,即点![]() 在以点
在以点![]() 为球心,半径为
为球心,半径为![]() 的球面上运动,
的球面上运动,
因此A、B选项不正确;
对于C选项,作![]() 可以看成以
可以看成以![]() 为轴线,以
为轴线,以![]() 为平面角的圆锥的母线,易知
为平面角的圆锥的母线,易知![]() 与
与![]() 落在同一个轴截面上时,
落在同一个轴截面上时,![]() 取得最大值,则
取得最大值,则![]() 的最大值为
的最大值为![]() ,此时
,此时![]() 落在平面
落在平面![]() 上,所以
上,所以![]() ,即
,即![]() 与
与![]() 所成的角始终小于
所成的角始终小于![]() ,所以C选项不正确;
,所以C选项不正确;
对于D选项,易知二面角![]() 为直二面角时,二面角
为直二面角时,二面角![]() 始终大于二面角
始终大于二面角![]() ,当二面角
,当二面角![]() 为锐二面角时,如图所示作
为锐二面角时,如图所示作![]() 平面
平面![]() 与点
与点![]() ,然后作
,然后作![]() 分别交
分别交![]() 于
于![]() ,
,
则二面角![]() 的平面角为
的平面角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,
,
且![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以二面角![]() 始终大于二面角
始终大于二面角![]() ,故选D.
,故选D.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知两动圆![]() 和
和![]() (
(![]() ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 满足:
满足:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明直线![]() 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.现有抛物线![]() ,如图一平行于
,如图一平行于![]() 轴的光线射向抛物线,经两次反射后沿平行
轴的光线射向抛物线,经两次反射后沿平行![]() 轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为![]() (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB为圆![]() 的一条直径,其端点A,B在抛物线
的一条直径,其端点A,B在抛物线![]() 上,且A,B两点到抛物线C焦点的距离之和为11.
上,且A,B两点到抛物线C焦点的距离之和为11.
(1)求抛物线C的方程及直径AB所在的直线方程;
(2)过M点的直线l交抛物线C于P,Q两点,抛物线C在P,Q处的切线相交于N点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为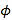 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com