
【题目】已知集合A={x|y= ![]() },B={x|x2﹣2x+1﹣m2≤0}.
},B={x|x2﹣2x+1﹣m2≤0}.
(1)若m=3,求A∩B;
(2)若m>0,AB,求m的取值范围.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠ ![]() .
.
(1)求c;
(2)若C= ![]() ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,sin2B=2sinAsinC.
(1)若a=b,求cosB的值;
(2)若B=60°,△ABC的面积为4 ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC的顶点都在圆O上,点P在BC的延长线上,且PA与圆O切于点A. 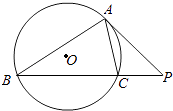
(1)若∠ACB=70°,求∠BAP的度数;
(2)若 ![]() =
= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣3|﹣|x﹣a|.
(1)当a=2时,解不等式f(x)≤﹣ ![]() ;
;
(2)若存在实数x,使得不等式f(x)≥a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量 ![]() =(1,bn),
=(1,bn), ![]() =(an﹣1,Sn),
=(an﹣1,Sn), ![]() ∥
∥ ![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若bn= ![]() ,a2=0.
,a2=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足cn= ![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn= ![]() (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com