练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,在Rt△ABC中,∠B=90°,tanC=,AB=a,在△ABC内作一系列的正方形,求所有这些正方形的面积和S.

    分析：这个题目的关键点是每一个小三角形都相似,据此可以写出Sn与an的关系式,经过化简,再求极限.

    解： 设第n个正方形的边长为an,则由三角形相似,可得(其中Sn=a1+a2+…+an).

    因为AB=a,tanC=,所以BC=2a.

    于是即Sn=2a-2an.

    当n≥2时,有an=Sn-Sn-1=-2an+2an-1,

    即3an=2an-1,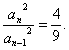

    因为tanC=,所以AB=a=a1+a1.

    所以a12=

    所以数列{an2}是首项为,公比为的无穷等比数列，

    S=(S1+S2+…+Sn)=

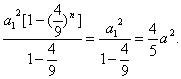
    点评：解决与无穷数列各项和有关的应用问题，关键是由题意找准首项、公比，求出前n项和，再求极限.对于形如qn的极限，当|q|<1时，可直接使用qn=0这一运算法则；当|q|>1时，可将分子、分母同除以增长“最快”的项,先转化形式,再求极限.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2
    		3
    ，则AC的长为（　　）
    A、2
    		2
    B、3
    C、
    		3
    D、
    3
    2
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
    （1）求证：点E是边BC的中点；
    （2）若EC=3，BD=2
    		6
    ，求⊙O的直径AC的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在Rt△ABC中，∠ABC=90°，BA=BC=2，AE⊥平面ABC，CD⊥平面ABC，CE交AD于点P．
    （1）若AE=CD，点M为BC的中点，求证：直线MP∥平面EAB
    （2）若AE=2，CD=1，求锐二面角E-BC-A的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    8．如图，在Rt△ABC中，∠CAB=90°，AB=2，AC=
    		2
    2
    ．DO⊥AB于O点，OA=OB，DO=2，曲线E过C点，动点P在E上运动，且保持|PA|+|PB|的值不变．
    （1）建立适当的坐标系，求曲线E的方程；
    （2）过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间，设
    DM
    DN
    =λ，试确定实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在Rt△ABC中，AC=1，BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是（　　）
    A、（0，
    		3
    ]
    B、（
    		2
    2
    ，2]
    C、（
    		3
    ，2
    		3
    ]
    D、（2，4]

    查看答案和解析>>

    同步练习册答案