
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: 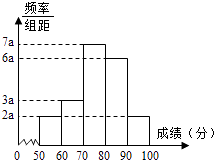
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.
【答案】
(1)解:根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)解:成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)解:记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P= ![]()
【解析】(1)根据频率分布直方图求出a的值;(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.(3)分别列出满足[50,70)的基本事件,再找到在[60,70)的事件个数,根据古典概率公式计算即可.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】知函数f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判断函数 f (x)的单调性;
(2)若函数 f (x)有两个极值点x1,x2,求证:f(x1)+f(x2)<﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a=log3650.99、b=1.01365、c=0.99365 , 则a、b、c的大小关系为( )
A.a<c<b
B.b<a<c
C.a<b<c
D.b<c<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+2x+c(a≠0),函数f(x)对于任意的都满足条件f(1+x)=f(1﹣x).
(1)若函数f(x)的图象与y轴交于点(0,2),求函数f(x)的解析式;
(2)若函数f(x)在区间(0,1)上有零点,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sin2x,2cos2x﹣1),
=(sin2x,2cos2x﹣1), ![]() =(sinθ,cosθ)(0<θ<π),函数f(x)=
=(sinθ,cosθ)(0<θ<π),函数f(x)= ![]()
![]() 的图象经过点(
的图象经过点( ![]() ,1).
,1).
(1)求θ及f(x)的最小正周期;
(2)当x∈ ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
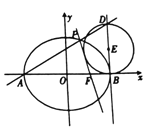
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人发现,多看电视容易使人变冷漠,如表是一个调查机构对此现象的调查结果:
冷漠 | 不冷漠 | 总计 | |
多看电视 | 68 | 42 | 110 |
少看电视 | 20 | 38 | 58 |
总计 | 88 | 80 | 168 |
P(K2≥k) | 0.025 | 0.010 | 0.005 | 0.001 |
k | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() ≈11.377,下列说法正确的是( )
≈11.377,下列说法正确的是( )
A.大约有99.9%的把握认为“多看电视与人变冷漠”有关系
B.大约有99.9%的把握认为“多看电视与人变冷漠”没有关系
C.某人爱看电视,则他变冷漠的可能性为99.9%
D.爱看电视的人中大约有99.9%会变冷漠
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是![]() .
.
(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量![]() 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求![]() 分布列及期望.
分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①幂函数f(x)= ![]() 的单调递减区间是(﹣∞,0)∪(0,+∞);
的单调递减区间是(﹣∞,0)∪(0,+∞);
②若函数f(x+2016)=x2﹣2x﹣1(x∈R),则函数f(x)的最小值为﹣2;
③若函数f(x)=loga|x|(a>0,a≠1)在(0,+∞)上单调递增,则f(﹣2)<f(a+1);
④若f(x)= ![]() 是(﹣∞,+∞)上的减函数,则a的取值范围是(
是(﹣∞,+∞)上的减函数,则a的取值范围是( ![]() ,
, ![]() );
);
⑤既是奇函数,又是偶函数的函数一定是f(x)=0(x∈R).
其中正确命题的序号有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com