
已知函数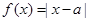 .
.
(1)若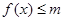 的解集为
的解集为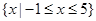 ,求实数
,求实数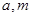 的值.
的值.
(2)当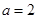 且
且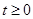 时,解关于
时,解关于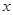 的不等式
的不等式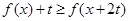 .
.
(1)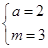 ;(2)当
;(2)当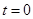 时,原不等式的解集为
时,原不等式的解集为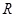 ,当
,当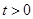 时,原不等式的解集为
时,原不等式的解集为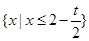 .
.
解析试题分析:本题考查绝对值不等式的解法及利用解集求实数的值,考查学生的分类讨论思想和转化能力.第一问,利用绝对值不等式的解法求出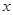 的范围,让它和已知解集相同,列出等式,解出
的范围,让它和已知解集相同,列出等式,解出 和
和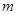 的值;第二问,先将
的值;第二问,先将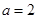 代入,得到
代入,得到 解析式,再代入到所求不等式中,找到需要解的不等式,注意到当
解析式,再代入到所求不等式中,找到需要解的不等式,注意到当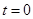 时,2个绝对值一样,所以先进行讨论,当
时,2个绝对值一样,所以先进行讨论,当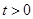 时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合
时,按照解绝对值不等式的步骤,先列出不等式组,内部求交集,综合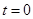 和
和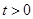 的情况得到结论.
的情况得到结论.
试题解析:(Ⅰ)由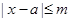 得
得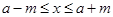 ,
,
所以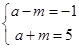 解之得
解之得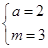 为所求. 4分
为所求. 4分
(Ⅱ)当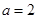 时,
时,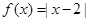 ,
,
所以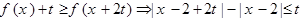
当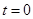 时,不等式①恒成立,即
时,不等式①恒成立,即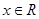 ;
;
当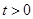 时,不等式
时,不等式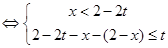 或
或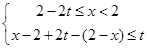 或
或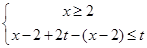 ,
,
解得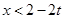 或
或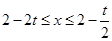 或
或 ,即
,即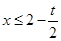 ;
;
综上,当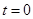 时,原不等式的解集为
时,原不等式的解集为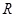 ,
,
当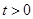 时,原不等式的解集为
时,原不等式的解集为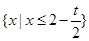 . 10分
. 10分
考点:1.绝对值不等式的解法.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com