
分析 (1)由分母x≠0,求出函数的定义域即可;(2)首先,任设两个变量,然后,作差比较,最后,得到结论.
解答 解:(1)由分母x≠0,得函数f(x)的定义域是{x|x≠0},
(2)任设x1,x2∈(0,+∞),
且x1<x2,
∴f(x1)-f(x2)=$\frac{1}{{x}_{1}}$-2-($\frac{1}{{x}_{2}}$-2)
=$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=$\frac{{x}_{2}{-x}_{1}}{{{x}_{1}x}_{2}}$,
∵x1<x2
∴x2-x1>0,
∴f(x1)-f(x2)>0,
∴函数f(x)=$\frac{1}{x}$-2在(0,+∞)上是减函数.
点评 本题主要考查函数的定义域问题,单调性的定义,借助于函数单调性定义求解时,一定要注意所取的自变量的任意性,属于基础题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | $\frac{e}{2}$ | C. | $\frac{{e}^{2}}{2}$ | D. | $\frac{{e}^{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
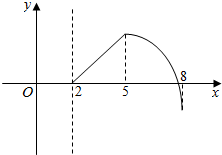 (1)写出函数y=x2-2x的单调区间及其图象的对称轴,观察:在函数图象对称轴两侧的单调性有什么特点?
(1)写出函数y=x2-2x的单调区间及其图象的对称轴,观察:在函数图象对称轴两侧的单调性有什么特点?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com