
【题目】已知函数![]() ,
,![]() ,
,
⑴ 若![]() 有零点,求 m 的取值范围;
有零点,求 m 的取值范围;
⑵ 确定 m 的取值范围,使得![]() 有两个相异实根.
有两个相异实根.
【答案】(1) ![]() ;(2)
;(2) ![]() ;
;
【解析】
(1) ![]() 在x>0时有根,再对
在x>0时有根,再对![]() (2)记
(2)记![]() ,证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,根据零点定理h(e)<0,解得
,证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,根据零点定理h(e)<0,解得![]() ,再证明在(e,+∞)上只有一个零点,在(0,e)上只有一个零点,综上即可得解.
,再证明在(e,+∞)上只有一个零点,在(0,e)上只有一个零点,综上即可得解.
(1) ![]() 在x>0有根,当
在x>0有根,当![]() 时则
时则![]() 或m≤-2e(舍),当
或m≤-2e(舍),当![]() 时,f(0)=e2,则f(0)≤0无解,则m≥2e.
时,f(0)=e2,则f(0)≤0无解,则m≥2e.
(2)记![]() ,
,
则可以证明h(x)在(0,e)上单调递减,在(e,+∞)上单调递增,证明如下:
任取![]() ,令
,令![]() ,
, ![]() 由于
由于![]() ,
, ![]() ,
, ![]() 所以
所以![]() ,所以函数在(0,e)上单调递减;同理可证得在(e,+∞)上单调递增,
,所以函数在(0,e)上单调递减;同理可证得在(e,+∞)上单调递增,
所以h(e)为函数最小值,根据零点定理h(e)<0,解得![]() ,
,
以下说明必存在函数值大于零:
首先说明(e,+∞)上,当m≥2e时, ![]() ,当
,当![]() 时,
时, ![]() ;所以在(e,+∞)上只有一个零点。
;所以在(e,+∞)上只有一个零点。
再说明(0,e)上, ![]() ,所以取
,所以取![]() 即中
即中![]() 中较小值,当
中较小值,当![]() 即
即![]() 时,
时, ![]() ;当
;当![]() 即
即![]() 时,
时, ![]() ;所以在(0,e)上只有一个零点。
;所以在(0,e)上只有一个零点。
综上, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=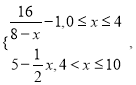 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,设
,设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)求![]() 的最小值及相应的
的最小值及相应的![]() 的值;
的值;
(2)设![]() ,若
,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,以
,以![]() 、
、![]() 、
、![]() 为三边长总能构成三角形,求
为三边长总能构成三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列![]() 个结论:
个结论:
①棱长均相等的棱锥一定不是六棱锥;
②函数![]() 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若函数![]() 满足条件
满足条件![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确的结论的序号是:______. (写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,左、右焦点分别为F1、F2,且|F1F2|=2,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A、B两点,且△AF2B的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=1,且an﹣1﹣an﹣1an﹣an=0(n≥2,n∈N*),记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 则满足不等式Tn< ![]() 成立的最大正整数n为 .
成立的最大正整数n为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.
(1)求点S到平面ABCD的距离;
(2)若E为SC的中点,求二面角A﹣DE﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海关对同时从![]() 三个不同地区进口的某种商品进行随机抽样检测,已知从
三个不同地区进口的某种商品进行随机抽样检测,已知从![]() 三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
(1)求这6件样品中,来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往另一机构进行进一步检测,求这2件样品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为  (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com