
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如下图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如下图所示,已知抽取的人员中成绩在[50,60)内的频数为3.

(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取1人,求这两人恰好都为女士的概率.
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取1人,求这两人恰好都为女士的概率.
【答案】(1)![]() ;平均成绩73.75; (2)
;平均成绩73.75; (2)![]()
【解析】
(1)由频率之和等于1得出成绩在![]() 频率,结合该组频数,得出抽取的样本容量,再由频率分布直方图中的数据估计参赛人员的平均成绩即可;
频率,结合该组频数,得出抽取的样本容量,再由频率分布直方图中的数据估计参赛人员的平均成绩即可;
(2)由频率分布直方图得出成绩在![]() 和
和![]() 抽取的人数,设抽取的40人中成绩在
抽取的人数,设抽取的40人中成绩在![]() 之间男士为
之间男士为![]() ,女士为
,女士为![]() ,成绩在
,成绩在![]() 之间的男士为
之间的男士为![]() ,女士为
,女士为![]() ,列举出成绩在
,列举出成绩在![]() ,
,![]() 的被抽取人员中各随机选取1人的所有情况,利用古典概型概率公式求解即可.
的被抽取人员中各随机选取1人的所有情况,利用古典概型概率公式求解即可.
(1)由频率分布直方图知,成绩在![]() 频率为
频率为![]()
![]() 成绩在
成绩在![]() 内频数为3,
内频数为3,![]() 抽取的样本容量
抽取的样本容量![]()
![]() 参赛人员平均成绩为
参赛人员平均成绩为![]() .
.
(2)由频率分布直方图知,抽取的人员中成绩在![]() 的人数为
的人数为![]()
成绩在![]() 的人数为
的人数为![]()
设抽取的40人中成绩在![]() 之间男士为
之间男士为![]() ,女士为
,女士为![]()
成绩在![]() 之间的男士为
之间的男士为![]() ,女士为
,女士为![]()
从成绩在![]() ,
,![]() 的被抽取人员中各随机选取1人,有{
的被抽取人员中各随机选取1人,有{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },
},
{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() }
}
共有20种不同取法,其中选中的2人中恰好都为女士的取法有{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() },{
},{![]() ,
,![]() }共4种不同取法,故选中的2人中恰好都为女士的概率为
}共4种不同取法,故选中的2人中恰好都为女士的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图a是某市参加2012年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为![]() 、
、![]() 、…、
、…、![]() [如
[如![]() 表示身高(单位:cm)在
表示身高(单位:cm)在![]() 内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在
内的学生人数].图b是统计图a中身高在一定范围内学生人数的一个算法流程图.现要统计身高在![]() (含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 为动点,以
为动点,以![]() 为直径的圆内切于
为直径的圆内切于![]() .
.
(1)证明![]() 为定值,并求点
为定值,并求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与
且与![]() 垂直,
垂直,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 的中点,求
的中点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 世纪中叶,中国数学家贾宪给出了直到六次幂的二项式系数表,如图所示是《杨辉详解九章算法》开方作法本原,其中第
世纪中叶,中国数学家贾宪给出了直到六次幂的二项式系数表,如图所示是《杨辉详解九章算法》开方作法本原,其中第![]() 层即为
层即为![]() 展开式的系数.贾宪称整张数表为“开放作法本原”,今称“贾宪三角”但贾宪未给出二项式系数的一般公式,因而未能建立一般正整数次幂的二项式定理.贾宪的数学著作已失传,
展开式的系数.贾宪称整张数表为“开放作法本原”,今称“贾宪三角”但贾宪未给出二项式系数的一般公式,因而未能建立一般正整数次幂的二项式定理.贾宪的数学著作已失传,![]() 世纪数学家杨辉在《详解九章算法》
世纪数学家杨辉在《详解九章算法》![]() 中引用了开放作法本原图,注明此图出“《释锁算数》,贾宪用此术”,因而流传至今.只是后人往往因此把它误称为“杨辉三角”.
中引用了开放作法本原图,注明此图出“《释锁算数》,贾宪用此术”,因而流传至今.只是后人往往因此把它误称为“杨辉三角”.![]() 展开式中
展开式中![]() 的系数为
的系数为![]() ,①则实数
,①则实数![]() 的值为_______________,②展开式中各项系数之和为__________________.
的值为_______________,②展开式中各项系数之和为__________________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: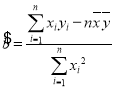 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com