
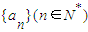 的前n项和为Sn,数列
的前n项和为Sn,数列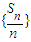 是首项为0,公差为
是首项为0,公差为 的等差数列.
的等差数列.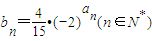 ,对任意的正整数k,将集合{b2k-1,b2k,b2k+1}中的三个元素排成一个递增的等差数列,其公差为dk,求dk;
,对任意的正整数k,将集合{b2k-1,b2k,b2k+1}中的三个元素排成一个递增的等差数列,其公差为dk,求dk;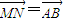 ,点N的轨迹是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x∈(0,3]时,g(x)=lgx,动点M的轨迹是函数f(x)的图象,求f(x).
,点N的轨迹是函数y=g(x)的图象,其中g(x)是以3为周期的周期函数,且当x∈(0,3]时,g(x)=lgx,动点M的轨迹是函数f(x)的图象,求f(x).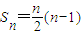 ,再根据前n项和与通项之间的关系即可求出数列{an}的通项公式;
,再根据前n项和与通项之间的关系即可求出数列{an}的通项公式;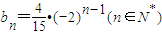 ,从而
,从而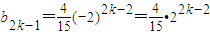 ,
,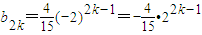
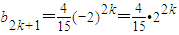 .最后由2b2k-1=b2k+b2k+1及b2k<b2k-1<b2k+1得b2k,b_2k-1g(x),b2k+1依次成递增的等差数列,即可求出公差为dk;
.最后由2b2k-1=b2k+b2k+1及b2k<b2k-1<b2k+1得b2k,b_2k-1g(x),b2k+1依次成递增的等差数列,即可求出公差为dk;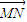 =
=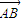 =(1,12)设当3m<x≤3(m+1)(m∈Z),有0<x-3m≤3,由是以3为周期的周期函数得,g(x)=g(x-3m)=lg(x-3m),再设M(x,y)是函数图象上的任意点,并设点N的坐标为(xN,yN),利用向量相等得到
=(1,12)设当3m<x≤3(m+1)(m∈Z),有0<x-3m≤3,由是以3为周期的周期函数得,g(x)=g(x-3m)=lg(x-3m),再设M(x,y)是函数图象上的任意点,并设点N的坐标为(xN,yN),利用向量相等得到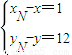 ,从而建立坐标之间的关系,即可求出求f(x).
,从而建立坐标之间的关系,即可求出求f(x).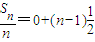 ,即
,即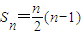
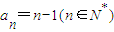 .
.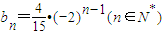 ,
,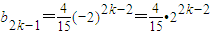 ,
,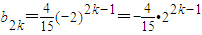
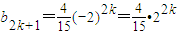 .
.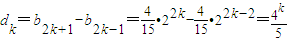 .
.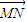 =
=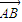 =(1,12)
=(1,12)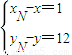 .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中数学 来源:2012届福建省高二下学期期末考试数学(文) 题型:解答题
(12分)已知数列 的前n项和为
的前n项和为 ,
, 且满足
且满足 =2
=2 +n (n>1且n∈
+n (n>1且n∈ )
)
(1)求数列 的通项公式和前n项的和
的通项公式和前n项的和
(2)设 ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值
查看答案和解析>>
科目:高中数学 来源:陕西省汉台区2009-2010学年高二第二学期期末考试(数学文)doc 题型:解答题
(本小题满分14分)
已知数列 的前n项和为
的前n项和为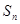 ,且
,且 ,
,
(1)试计算 ,并猜想
,并猜想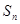 的表达式;
的表达式;
(2) 证明你的猜想,并求出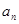 的表达式。
的表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com