
【题目】如图,在三棱锥P﹣ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P﹣AC﹣B的大小为60°; 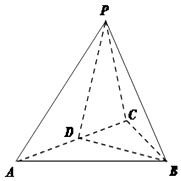
(1)求证:平面PBD⊥平面PAC;
(2)求AB与平面PAC所成角的正弦值.
【答案】
(1)证明:∵BD⊥AC,PD⊥AC,BD∩PD=D,
∴AC⊥面PBD,
又AC面PAC,所以 面PAC⊥面PBD,
即平面平面PBD⊥平面PAC
(2)解:如图建立空间直角坐标系,则D(0,0,0),
令A(1,0,0),则B(0, ![]() ,0),C(﹣1,0,0),
,0),C(﹣1,0,0),
又∠PDB为二面角P﹣AC﹣B的平面角,得∠PDB=60°,
设DP=λ,则P(0, ![]() ,
, ![]() λ),
λ),
设 ![]() =(x,y,z)为面PAC的法向量,则
=(x,y,z)为面PAC的法向量,则 ![]() =(﹣2,0,0),
=(﹣2,0,0), ![]() =(﹣1,
=(﹣1, ![]() ,
, ![]() λ),
λ),
得 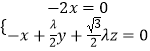 取y=
取y= ![]() ,得
,得 ![]() =(0,
=(0, ![]() ,﹣1),
,﹣1),
又 ![]() =(﹣1,
=(﹣1, ![]() ,0)得 cos<
,0)得 cos< ![]() ,
, ![]() >=
>= ![]() ,
,
∴AB与平面PAC所成角的正弦值为 ![]() .
.

【解析】(1)证明AC⊥面PBD,即可证明平面PBD⊥平面PAC;(2)求出面PAC的法向量,利用向量的方法求AB与平面PAC所成角的正弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域是(0,+∞),对于任意正实数m,n恒有f(mn)=f(m)+f(n),且当x>1时,f(x)>0,f(2)=1.
(1)求 ![]() 的值;
的值;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)求方程4sinx=f(x)的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 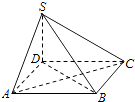
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用随机数表法对一个容量为500编号为000,001,002,…,499的产品进行抽样检验,抽取一个容量为10的样本,若选定从第12行第5列的数开始向右读数,(下面摘取了随机数表中的第11行至第15行),根据下图,读出的第3个数是( ) 
A.841
B.114
C.014
D.146
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com