分析:(Ⅰ)利用线面垂直的判定定理即可证明;
(Ⅱ)通过空间直角坐标系,分别求出平面CA1D1的法向量及斜线AP的向量坐标,进而求出其夹角,即可解决问题.
解答:解:(Ⅰ)∵A
1B
1=A
1C
1,点D
1是棱B
1C
1的中点.
∴A
1D
1⊥B
1C
1,
又∵BB
1⊥平面A
1B
1C
1,∴BB
1⊥B
1C
1,
又∵BB
1∩B
1C
1,
∴A
1D
1⊥平面BB
1C
1C.
(Ⅱ)建立如图所示的空间直角坐标系,∵AB=AC=AA
1=2,
∴A(0,0,0),A
1(0,0,2),C(0,-2,0),C
1(0,-2,2),B
1(-2,0,2),D
1(-1,-1,2).
=(0,2,2),
=(-1,1,2),
设平面A
1D
1C的法向量
=(x,y,z),
则
即
,
令y=-1,则z=1,x=1,∴
=(1,-1,1).
设
=λ,0≤λ≤1,
∵
=(-2,0,0),∴
=(-2λ,0,0),P(-2λ,0,2),
=(-2λ,0,2).
∵直线AP与平面A
1D
1C所成角的正弦值为
,
∴
=
|cos<,>|=
=
,
化为3λ
2-10λ+3=0,解得
λ=或3.
∵0≤λ≤1,
∴
λ=,即
=.
点评:熟练掌握线面垂直的判定定理和通过建立空间直角坐标系求出法向量与斜向量的夹角是解决问题的关键.

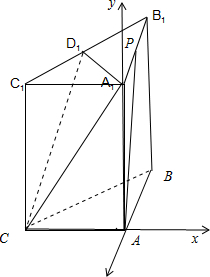
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.