

(1)求侧棱AA1与平面AB1C所成角的大小;
(2)已知点D满足BD=BA+BC,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
(文)如图,在各棱长均为2的三棱柱ABC—A1B1C1中,点A1在底面ABC内的射影O恰为线段AC的中点.

(1)求侧棱AA1与平面AB1C所成角的正弦值;
(2)已知点D为点B关于点O的对称点,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
答案:(理)解:(1)∵侧面A1ACC1⊥底面ABC,作A1O⊥AC于点O,

∴A1O⊥平面ABC.又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB=![]() ,BO⊥AC.
,BO⊥AC.
故以O为坐标原点,建立如图所示的空间直角坐标系O—xyz,则A(0,-1,0),B(![]() ,0,0),A1(0,0,
,0,0),A1(0,0,![]() ),C(0,1,0),
),C(0,1,0),![]() =(0,1,
=(0,1,![]() ).由
).由![]() =
=![]() ,可得B1(
,可得B1(![]() ,1,
,1,![]() ).
).
∴![]() =(
=(![]() ,2,
,2,![]() ),
),![]() =(0,2,0).设平面AB1C的法向量为n=(x,y,1).
=(0,2,0).设平面AB1C的法向量为n=(x,y,1).
则 解得n=(-1,0,1).
解得n=(-1,0,1).
由cos〈![]() ,n〉=
,n〉=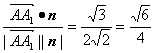 ,
,
而侧棱AA1与平面AB1C所成角,即是向量![]() 与平面AB1C的法向量所成锐角的余角,
与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的大小为arcsin![]() .
.
(2)∵![]() ,而BA=(
,而BA=(![]() ,-1,0),
,-1,0),![]() =(
=(![]() ,1,0),∴
,1,0),∴![]() =(
=(![]() ,0,0).
,0,0).
又∵B(![]() ,0,0),∴点D的坐标为D(
,0,0),∴点D的坐标为D(![]() ,0,0).
,0,0).
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).∴![]() =(
=(![]() ,y,z).
,y,z).
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,∴由![]() ·n=
·n=![]() +0+z=0,得z=
+0+z=0,得z=![]() .
.
又∵点P在直线AA1上,![]() =(0,y+1,
=(0,y+1,![]() ),
),![]() =(0,1,
=(0,1,![]() ),∴由
),∴由![]() ,得
,得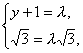 ∴y=0.又DP
∴y=0.又DP![]() 平面AB1C,故存在点P,使DP∥平面AB1C,其坐标为(0,0,
平面AB1C,故存在点P,使DP∥平面AB1C,其坐标为(0,0,![]() ),即恰好为A1点.
),即恰好为A1点.
(文)解:(1)连结A1O,则A1O⊥平面ABC.

∵三棱柱各棱长都相等,∴AO=1,OA1=OB=![]() ,BO⊥AC.
,BO⊥AC.
故以O为坐标原点,建立如图所示的空间直角坐标系O—xyz,则A(0,-1,0),B(![]() ,0,0),A1(0,0,
,0,0),A1(0,0,![]() ),C(0,1,0),
),C(0,1,0),![]() =(0,1,
=(0,1,![]() ).由
).由![]() ,可得B1(
,可得B1(![]() ,1,
,1,![]() ).
).
∴![]() =(
=(![]() ,2,
,2,![]() ),
),![]() =(0,2,0).设平面AB1C的法向量为n=(x,y,1).则
=(0,2,0).设平面AB1C的法向量为n=(x,y,1).则 解得n=(-1,0,1).
解得n=(-1,0,1).
∴cos〈![]() ,n〉=
,n〉=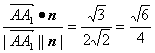 .
.
而侧棱AA1与平面AB1C所成角,即是向量![]() 与平面AB1C的法向量所成锐角的余角,
与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的正弦值为![]() .
.
(2)∵BO⊥AC,点D为点B关于点O的对称点,∴点D的坐标为D(![]() ,0,0).
,0,0).
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).∴![]() =(
=(![]() ,y,z).
,y,z).
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,∴由![]() ·n=-
·n=-![]() +0+z=0,得z=
+0+z=0,得z=![]() .
.
又∵点P在直线AA1上,![]() =(0,y+1,
=(0,y+1,![]() ),
),![]() =(0,1,
=(0,1,![]() ),
),
∴由![]() ,得
,得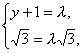 ∴y=0.又DP
∴y=0.又DP![]() 平面AB1C,
平面AB1C,
故存在点P,使DP∥平面AB1C,其坐标为(0,0,![]() ),即恰好为A1点.
),即恰好为A1点.


科目:高中数学 来源:2008年高考预测卷数学科(二)新课标 题型:044
(理)如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
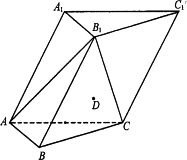
(Ⅰ)求侧棱AA![]() 与平面AB
与平面AB![]() C所成角的正弦值的大小;
C所成角的正弦值的大小;
(Ⅱ)已知点D满足![]() ,在直线AA
,在直线AA![]() 上是否存在点P,使DP∥平面AB
上是否存在点P,使DP∥平面AB![]() C?若存在,请确定点P的位置;若不存在,请说明理由.
C?若存在,请确定点P的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
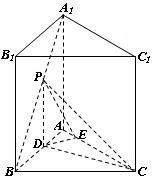
(09年湖北八校联考理)(12分)如图,已知正三棱柱![]() 各棱长都为
各棱长都为![]() ,
,![]() 为棱
为棱![]() 上的动点。
上的动点。
(Ⅰ)试确定![]() 的值,使得
的值,使得![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(Ⅲ)在(Ⅱ)的条件下,求点![]() 到面
到面![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鄂尔多斯市一模理) 如图,在各棱长都为2的正三棱柱ABC―A1B1C1中,![]() 的重心.
的重心.
(1)求证:DG//平面ABC;
(2)求二面角B―AG―C的大小;
(3)求点B1到平面AGC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求侧棱AA1与平面AB1C所成角的大小;
(2)已知点D满足BD=BA+BC,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.(文)如图,在各棱长均为2的三棱柱ABC—A1B1C1中,点A1在底面ABC内的射影O恰为线段AC的中点.
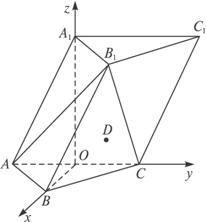
(1)求侧棱AA1与平面AB1C所成角的正弦值;
(2)已知点D为点B关于点O的对称点,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com