
以下是某地搜集到的新房屋的销售价格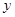 (万元)和房屋的面积
(万元)和房屋的面积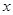 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知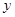 对
对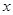 呈线性相关关系。
呈线性相关关系。
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为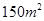 时的销售价格.
时的销售价格.
参考公式: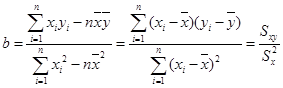
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下
表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文
科学生总成绩不好与数学成绩不好有关系吗?
| | 总成绩好 | 总成绩不好 | 总计 |
| 数学成绩好 | 20 | 10 | 30 |
| 数学成绩不好 | 5 | 15 | 20 |
| 总计 | 25 | 25 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的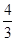 倍.
倍.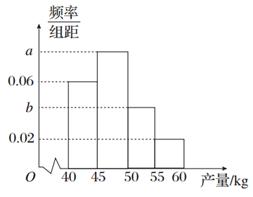
(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树中随机抽取2株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
. ,其中
,其中 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•广东)在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查民营企业的经营状况,某统计机构用分层抽样的方法从A、B、C三个城市中,抽取若干个民营企业组成样本进行深入研究,有关数据见下表:(单位:个)
| 城市 | 民营企业数量 | 抽取数量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
 、
、 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•重庆)从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得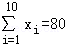 ,
, ,
, ,
,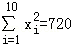 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, ,
,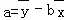 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·泰安模拟)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间 (分钟) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 人数 | 40 | 60 | 80 | 100 | 80 | 40 |
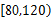 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?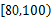 分钟内的概率.
分钟内的概率. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用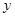 (万元),有如下的统计资料:
(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
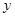 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com