
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设![]() 的内角
的内角![]() 的对应边分别为
的对应边分别为![]() ,且
,且![]() ,若向量
,若向量![]() 与向量
与向量![]() 共线,求
共线,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用三角函数的恒等变换化简f(x)的解析式为![]() .令
.令![]() ,k∈z,求得x的范围,结合
,k∈z,求得x的范围,结合![]() ,可得f(x)的递增区间.
,可得f(x)的递增区间.
(2)由f(C)=2,求得![]() ,结合C的范围求得C的值.根据向量
,结合C的范围求得C的值.根据向量![]() =(1,sinA)与向量
=(1,sinA)与向量![]() =(2,sinB)共线,可得
=(2,sinB)共线,可得 ![]() ,故有
,故有![]() =
=![]() ①,再由余弦定理得9=a2+b2﹣ab ②,由①②求得a、b的值.
①,再由余弦定理得9=a2+b2﹣ab ②,由①②求得a、b的值.
(1)∵![]() =
=![]() =
=![]() .
.
令![]() ,
,
解得![]() ,即
,即![]() ,
,
∵![]() ,∴f(x)的递增区间为
,∴f(x)的递增区间为![]() .
.
(2)由![]() ,得
,得![]() .
.
而C∈(0,π),∴![]() ,∴
,∴![]() ,可得
,可得![]() .
.
∵向量向量![]() =(1,sinA)与向量
=(1,sinA)与向量![]() =(2,sinB)共线,∴
=(2,sinB)共线,∴![]() ,
,
由正弦定理得:![]() =
=![]() ①.
①.
由余弦定理得:c2=a2+b2﹣2abcosC,即9=a2+b2﹣ab ②,
由①、②解得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣cos2x﹣2![]() sinxcosx(x∈R).
sinxcosx(x∈R).
(1)求f(x)的单调递增区间;
(2)求函数f(x)在区间[![]() ,
,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
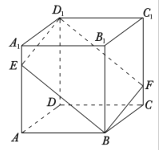
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由四个不同的数字![]() 1,2,4,
1,2,4,![]() 组成无重复数字的三位数.(最后的结果用数字表达)
组成无重复数字的三位数.(最后的结果用数字表达)
(Ⅰ)若![]() ,其中能被5整除的共有多少个?
,其中能被5整除的共有多少个?
(Ⅱ)若![]() ,其中能被3整除的共有多少个?
,其中能被3整除的共有多少个?
(Ⅲ)若![]() ,其中的偶数共有多少个?
,其中的偶数共有多少个?
(Ⅳ)若所有这些三位数的各位数字之和是252,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京联合张家口获得2022年第24届冬奥会举办权,我国各地掀起了发展冰雪运动的热潮,现对某高中的学生对于冰雪运动是否感兴趣进行调查,该高中男生人数是女生的1.2倍,按照分层抽样的方法,从中抽取110人,调查高中生“是否对冰雪运动感兴趣”得到如下列联表:
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
(1)补充完成上述![]() 列联表;
列联表;
(2)是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附:![]() (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,E,F分别为线段AB,BC的中点.
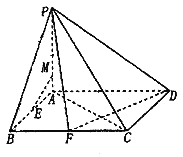
(1)线段AP上一点M,满足![]() ,求证:EM∥平面PDF;
,求证:EM∥平面PDF;
(2)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com