
【题目】设![]() ,
,![]() 。
。
(1)求![]() 的单调区间;
的单调区间;
(2)讨论![]() 零点的个数;
零点的个数;
(3)当![]() 时,设
时,设![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 。(2)见解析;(3)
。(2)见解析;(3) ![]()
【解析】
(1)直接对原函数求导,令导数大于0,解得增区间,令导数小于0,解得减区间;
(2)先判断![]() 是f(x)的一个零点,当
是f(x)的一个零点,当![]() 时,由f(x)=0得,
时,由f(x)=0得,![]() ,对函数
,对函数![]() 求导得
求导得![]() 的大致图像,分析y=a与
的大致图像,分析y=a与![]() 交点的个数可得到函数f(x)的零点个数.
交点的个数可得到函数f(x)的零点个数.
(3)不等式恒成立转化为函数的最值问题,通过变形构造出函数h(x)=f(x)-ag(x),通过研究该函数的单调性与极值,进而转化为该函数的最小值大于等于0恒成立,求得a即可.
(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增,当
递增,当![]() 时,
时,![]() ,g(x)递减,
,g(x)递减,
故![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() 是f(x)的一个零点,当
是f(x)的一个零点,当![]() 时,由f(x)=0得,
时,由f(x)=0得,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 递减且
递减且![]() ,
,
当![]() 时,
时,![]() ,且
,且![]() 时,
时,![]() 递减,
递减,
![]() 时,
时,![]() 递增,故,
递增,故,![]() ,
,
大致图像如图,
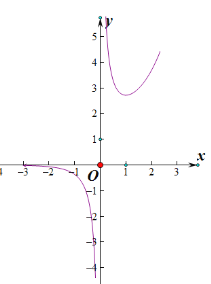
∴当![]() 时,f(x)有1个零点;
时,f(x)有1个零点;
当a=e或![]() 时,f(x)有2个零点;;
时,f(x)有2个零点;;
当![]() 时,
时, ![]() 有3个零点.
有3个零点.
(3)h(x)=f(x)-ag(x)=x![]() ,
,
![]() ,
,
![]() 设
设![]() 的根为
的根为![]() ,即有
,即有
![]() ,可得
,可得![]() ,
,![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
![]()

![]() ,
,
∴ ![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.设有一个回归方程![]() ,变量x增加1个单位时,y平均减少5个单位
,变量x增加1个单位时,y平均减少5个单位
C.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),则P(ξ>1)=0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 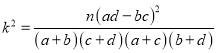 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD外切于![]() ,△ACB的内切圆
,△ACB的内切圆![]() 与边AB、BC的切点分别为P、Q,,△ACD的内切圆
与边AB、BC的切点分别为P、Q,,△ACD的内切圆![]() 与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为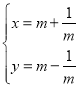 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com