函数f(x)的定义域为{x|x∈R,且x≠1},已知f(x+1)为奇函数,当x<1时,f(x)=2x2-x+1,则当x>1时,f(x)的递减区间是 ________
[

,+∞)
分析:由f(x+1)为奇函数,利用换元法得f(x)=-f(2-x),再设x>1,则2-x<1,代入解析式求出f(2-x),由关系式求出
f(x),根据二次函数的单调性求出它的减区间.
解答:由题意知,f(x+1)为奇函数,则f(-x+1)=-f(x+1),
令t=-x+1,则x=1-t,故f(t)=-f(2-t),即f(x)=-f(2-x),
设x>1,则2-x<1,
∵当x<1时,f(x)=2x
2-x+1,∴f(2-x)=2(2-x)
2-(2-x)+1=2x
2-7x+7,
∴f(x)=-f(2-x)=-2x
2+7x-7,∴函数的对称轴x=

故所求的减区间是
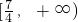
.
故答案为:
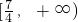
.
点评:本题主要考查对单调性和奇偶性的理解,判断函数奇偶性和求函数单调区间的基本方法以及函数解析式的求解方法的掌握,关键利用奇函数的定义推出的关系式;并且函数的单调性、奇偶性是高考函数题的重点考查内容.

 ,+∞)
,+∞)
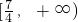 .
.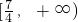 .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案