
【题目】设函数![]()
(1)当a=b=1时,求函数f(x)的图象在点(e2,f(e2))处的切线方程;
(2)当b=1时,若存在![]() ,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
,使f(x1)≤f'(x2)+a成立,求实数a的最小值.
【答案】(1)3x+4y﹣e2=0(2)![]()
【解析】
(1)求![]() ,即可求解;
,即可求解;
(2)存在![]() ,使f(x1)≤f'(x2)+a成立,转化为
,使f(x1)≤f'(x2)+a成立,转化为![]() ,通过配方法求出
,通过配方法求出![]() ,对
,对![]() 分类讨论,确定
分类讨论,确定![]() 的单调性或求出
的单调性或求出![]() 的极小值,进而求出
的极小值,进而求出![]() 的最小值,即可求解.
的最小值,即可求解.
(1)当a=b=1时,f(x)![]() ,
,![]() ,
,
![]() ,f'(e2)
,f'(e2)![]() ,
,
故函数f(x)的图象在点(e2,f(e2))处的切线方程为3x+4y﹣e2=0;
(2)当b=1时,f(x)![]() ,
,
![]() ,
,
设![]()
![]() ,
,
当x∈[e,e2]时,![]() ,g(x)
,g(x)![]() ,
,
故存在![]() ,使
,使![]() 成立,
成立,
只需x∈[e,e2],![]() 即可,下面求f(x)的最小值,
即可,下面求f(x)的最小值,
由于![]() ,
,
当a![]() 时,f'(x)≤0,f(x)在[e,e2]递减,
时,f'(x)≤0,f(x)在[e,e2]递减,
![]() ,得
,得![]() ;
;
当![]() 时,x∈[e,e2],
时,x∈[e,e2],
由于![]() ,
,
若﹣a≥0,即f'(x)≥0,f(x)递增,
![]() ,故不成立;
,故不成立;
若﹣a<0,即0<a![]() ,根据复合函数的单调性,
,根据复合函数的单调性,
f'(x)在[e,e2]单调递增,存在唯一零点m∈(e,e2),
f'(m)=0,使得f(x)在[e,m],f'(x)<0,f(x)递减;
f(x)在(m,e2],f'(x)>0,f(x)递增;
故f(x)![]() ,m∈(e,e2),
,m∈(e,e2),
若![]() 成立,即
成立,即![]() 成立,
成立,
设![]() ,x∈(e,e2),
,x∈(e,e2),
![]() 递减,
递减,
所以![]() ,
,
所以不成立;
综上,![]() ,
,
故a的最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
(1)根据已知条件完成下面的2×2列联表,并判断能否有97.5%的把握认为犹豫与否与性别有关;
犹豫 | 不犹豫 | 总计 | |
男性青年 |
|
|
|
女性青年 |
|
|
|
总计 |
|
| 1800 |
(2)以表中频率作为概率,若从街头随机采访青年男女各2人,求4人中“响应”的人数恰好是“不响应”的人数(“不响应”的人数不为0)的2倍的概率.
参考公式: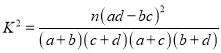
参考数据:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E为PB中点.利用空间向量方法完成以下问题:
,E为PB中点.利用空间向量方法完成以下问题:
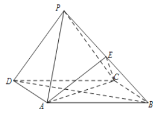
(1)求二面角E-AC-D的余弦值;
(2)在棱PD上是否存在点M,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,直线
轴不重合,直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过![]() 、
、![]() 、
、![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,证明直线
两点,证明直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com